Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 1.1 - Ex. 16
Em 1989, cientistas da IBM movimentaram átomos com um microscópio de tunelamento com varredura (scanning tunneling microscope, STM). Uma das primeiras imagens vistas pelo público em geral foi a das letras IBM traçadas com átomos de xenônio sobre uma superfície de níquel. As letras IBM se estendiam por átomos de xenônio. Se a distância entre os centros de átomos de xenônio adjacentes é (, estime quantas vezes “IBM” poderia ter sigo escrito nessa página de polegadas de largura.
Passo 1
Cara, vamos entender o que ele quis dizer primeiro? Vamos! A ideia é que a palavra IBM foi escrita usando átomos. E o espaço ocupado pela palavra é o espaço que 15 átomos de xenômio ocupariam. Algo assim:
Ele diz a distância entre os centros desses átomos, quando um está do lado do outro(adjacentes).
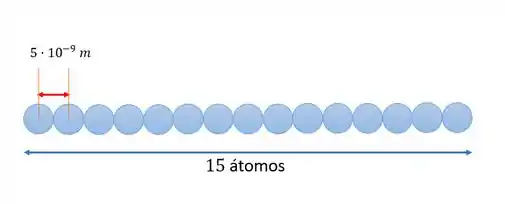
Se a palavra “IBM” se estende por átomos de xenônio, e a distância entre os centros de átomos adjacentes é , podemos calcular a largura total ocupada pela palavra:
Aí o que o enunciado quer saber?
Ele quer saber quantas vezes a gente poderia escrever IBM, dessa forma, no espaço de uma folha do livro (vamos considerar que é uma folha A4). Considerando que a folha está vertical, a gente iria escrever na direção paralela a largura da folha, que é de .
Então a ideia é quantas vezes conseguimos escrever a palavra IBM com átomos numa largura de . Vamos ver!
Passo 2
Vimos que a página do livro tem polegadas de largura . Vamos converter para metros porque nossa largura da palavra está em metros. Essa é a relação entre polegadas e metro
A tiramos do apêndice A. Como :
Daí vemos que para sair de polegadas e chegar a metros a gente multiplica o nosso valor pelo fator , assim:
E então quantas palavras cabem nessa largura? Para descobrir, a gente vai dividir essa largura pela largura da palavra IBM:
Resposta
A palavra poderia ser escrita na página aproximadamente (três milhões) de vezes.