Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 23.Exercícios - Ex. 45
Uma esfera metálica com raio está apoiada sobre uma base isolante no centro de uma casca esférica metálica com raio externo . Uma carga é colocada na esfera interna e uma carga , na esfera externa. O módulo de é escolhido para produzir uma diferença de potencial entre as esferas igual a , mantendo a esfera interna
com um potencial mais elevado. Use o resultado do Exercício para calcular o valor de . Com base no resultado do Exercício , faça um desenho indicando as superfícies equipotenciais que correspondem a , , , , e . Em seu desenho, mostre as linhas de campo elétrico. As linhas de campo elétrico e as superfícies equipotenciais são mutuamente perpendiculares? As superfícies equipotenciais ficam mais próximas entre si quando o módulo de é mais elevado?
Passo 1
Vem comigo que a gente resolve essa juntos!
O item quer que calculemos usando o resultado do exercício , esse exercício nos dá que a diferença de potencial entre o ponto e o ponto é:
Onde , já que e .
Então podemos isolar nessa equação e calcular seu valor.
O item quer que usemos o resultado do exercício para desenharmos as linhas equipotenciais. Temos o seguinte:
Para :
Para :
Para :
Nós vamos usar essas equação para saber a posição das equipotenciais que o item pede.
O item pede para desenharmos as linhas de campo, para isso temos que lembrar que o campo de uma esfera carregada é radial.
Vamos lá então!
Passo 2
Começando com o item .
Temos o seguinte:
Substituindo os valores que conhecemos, temos:
Então temos que:
Passo 3
Agora vamos para o item , antes de desenhar nossas equipotenciais, temos que saber as posições delas.
Primeiro pra .
Como a esfera interna é condutora, a sua superfície é uma equipotencial, no caso .
Para .
Podemos usar a equação para a região , temos que:
Então temos que:
Para .
Podemos usar a equação para a região , temos que:
Então temos que:
Passo 4
Para .
Podemos usar a equação para a região , temos que:
Então temos que:
Para .
Podemos usar a equação para a região , temos que:
Então temos que:
E para a equipotencial ocorre em já que a casca esférica é condutora.
Passo 5
Levando todas essas equipotenciais em consideração, temos a seguinte figura:
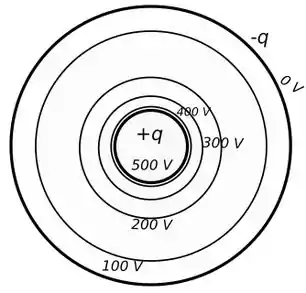
Passo 6
Agora vamos para o item .
Como falamos no passo o campo elétrico de uma esfera carregada é radial, então temos o seguinte:
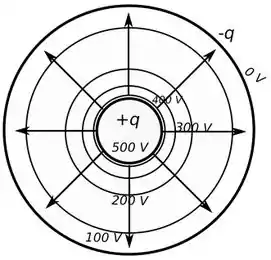
Como podemos ver pela figura as linhas de campo são perpendiculares as equipotenciais. E as equipotenciais ficam mais próximas onde o campo é mais elevado.
Resposta
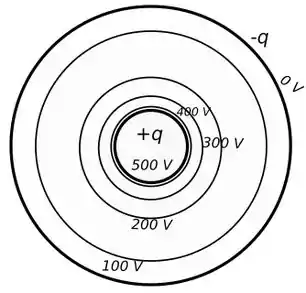
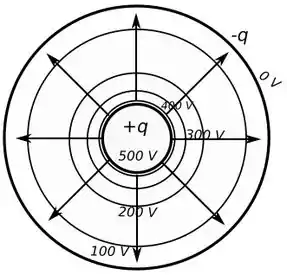
Explicado acima.