Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 35.Problemas - Ex. 50
50. Considere uma experiência de interferência com duas fendas de larguras diferentes. Fazendo-se medidas em uma tela muito afastada, a amplitude da onda proveniente da primeira fenda é igual a , enguanto a amplitude da onda proventente da segunda fenda é
igual a . Mostre que a intensidade em qualquer ponto da figura
de interferência é dada por
onde é a diferença de fase entre as duas ondas medidas em um ponto particular da tela e é a intensidade máxima da figura de interferência. Faça um gráfico de por (como na Figura ). Qual é o valor mínimo da intensidade e para quais valores
de isso ocorre?
Passo 1
Vamos começar com isso meu povo!
Primeiro, para mostramos o que o item quer vamos usar a seguinte equação da página do livro, temos:
Onde representa a onda emitida por uma fenda e representa a onda emitida pela outra fenda.
Tendo isso vamos usar também a seguinte equação para encontrarmos a intensidade , temos:
Com essas informações conseguimos mostrar o que o enunciado quer.
Depois temos que fazer um gráfico dessa expressão que vamos encontrar em para .
Depois também vamos analisar o valor mínimo de .
Passo 2
Vamos lá então galera, temos o seguinte:
Lembrando que segundo enunciado temos e , temos:
Agora substituindo isso na seguinte equação:
Temos:
Agora vamos fazer o seguinte, para temos , assim ficamos com:
Vamos chamar essa grandeza de e vamos isolá-la na nossa equação, assim ficamos com:
Como o enunciado queria.
Passo 3
Agora vamos fazer o gráfico que o enunciado pete, temos então o seguinte gráfico:
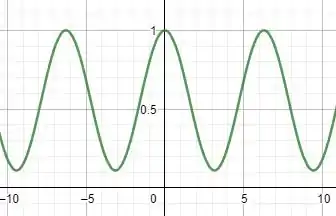
Então galera o menor valor de analisando a equação:
É encontrado toda vez que , pois assim , então temos:
Resposta
