55. Um detector e uma fonte de luz monocromática estão separados por uma distância , estando ambos localizados no ar a uma distância acima de uma placa plana de vidro. As ondas que atingem diretamente de sofrem interferência com as ondas refletidas na superfície do vidro. A distância é pequena em comparação com , de modo que a reflexão é próxima da normal. Mostre que a condição de interferência construtiva é e que a condição de interferência destrutiva é . (Sugestão: leve em consideração a mudança de fase que ocorre na reflexão.) Seja e . Qual é o comprimento de onda mais longo para o qual pode ocorrer interferência construtiva?
Passo 1
Para conseguimos entender, melhor a situação, vamos desenhar o que está acontecendo, temos seguinte desenho do que é descrito pelo enunciado:
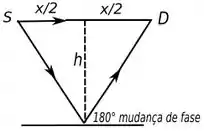
Como você pode reparar temos uma mudança de fase de quando temos a reflexão.
Com isso a condição para interferência construtiva é dada pela igualdade entre a diferença de caminho e .
A interferência destrutiva é dada pela igualdade entre a diferença de caminho e .
E o que seria essa diferença de caminho que mencionei? Então, é a diferença entre os trajetos que a luz toma para chegar no ponto .
Agora para responder o item vamos pegar a expressão para interferência construtiva e calcular o valor de para .
Passo 2
Vamos então encontrar a distância percorrida pela luz nos dois caminhos e fazer a diferença.
O caminho direto de até sem reflexão é tranquilo de achar, temos que:
Agora para o caminho que tem reflexão vamos usar a o teorema de Pitágoras ao nosso favor, assim temos:
Podemos colocar esse para dentro da raiz, assim:
Fazendo a diferença de caminhos temos:
Passo 3
Agora vamos aplicar isso as condições de interferência construtiva e destrutiva, temos então o seguinte.
Interferência construtiva:
Interferência destrutiva:
Passo 4
Agora vamos para o item , temos o seguinte:
Substituindo os valores que conhecemos, temos:
Temos então que:
Resposta
Interferência construtiva:
Interferência destrutiva: