Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.5 - Ex. 55
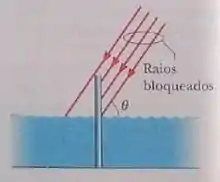
Passo 1
Vamos fazer um desenho para melhor visualizar:
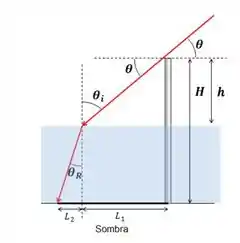
A sombra é dividida em duas partes: e . Pelo desenho temos que:
Precisamos dos ângulos!
Passo 2
O ângulo de incidência vai ser: e o ângulo de refração é dado pela lei de Snell:
Passo 3
Agora que sabemos os ângulos, podemos calcular as sombras! Do passo 1:
Sendo assim a sombra vai ser:
Resposta
Exercícios de Livros Relacionados
Um raio de luz que estava se propagando no vácuo incide na superfície de uma placa de vidro. No vácuo, o raio faz um ângulo de 32,0 ° com a normal à superfície, enquanto no vidro faz um ângulo de 21,0
Na Fig. 33-52a, um feixe luminoso que estava se propagando no meio 1 incide no meio 2 com um ângulo de 30 ° . A refração da luz no meio 2 depende, entre outros fatores, do índice de refração n 2 do me
Quando um tanque retangular de metal da Fig 33-46 está cheio até a borda de um líquido desconhecido, um observador O, com os olhos ao nível do alto do tanque , mal pode ver o vértice E. A figura mostr
Na Fig. 33-50a, um feixe luminoso que estava se propagando no meio 1 incide com um ângulo θ 140 ° na interface com o meio 2. Parte da luz penetra no meio 2 e parte dessa luz penetra no meio 3; todas a
Na Fig. 33-48a, um raio luminoso que estava se propagando na água incide com um ângulo θ 1 em outro meio, no qual parte da luz se refrata. O outro meio pode ser do tipo 1 ou do tipo 2; a Fig. 33-48b m