9.13. A força de atração gravitacional entre dois corpos de massa m e M é
onde r é a distância entre eles e G é a constante universal de gravitação. Como a força elétrica entre duas partículas carregadas, essa força também varia com
a. Faça uma analogia com o Problema 8 e escreva a fórmula da energia potencial gravitacional U(r) associada à força F.
b. Faça o gráfico de U em função de r.
c. Para qual valor de r a energia potencial U é nula?
d. Qual o menor valor da energia total E desses dois corpos para que eles possam se afastar indefinidamente?
Passo 1
Beleza, vamos para o item (a).
A energia potencial pode ser obtida através da integração da força:
Isso fica:
Passo 2
Agora vamos para o item (b).
O gráfico é uma hipérbole, que vai com . Então o formato do gráfico é o seguinte:
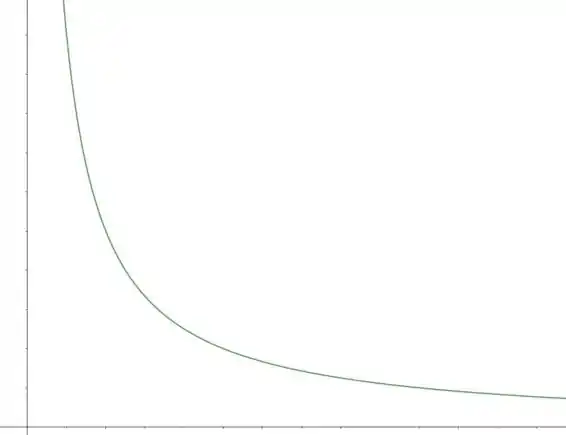
Passo 3
Agora vamos para o item (c).
Bom, a energia potencial é
Para que seja , então . Não temos um valor para em que , mas no limite em que vai para o infinito, então .
Passo 4
Finalmente vamos para o item (d).
Bom, o maior valor de para qual os corpos ainda se atraem vai ser aquele logo antes de um dos corpos atingir a velocidade de escape:
Então:
Mas olha só, isso é exatamente o valor de .
Em outras palavras os corpos param de se atrair quando . Então a menor energia é .