Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
(a) Se a aceleração máxima que pode ser tolerada pelos passageiros de um metrô é e duas estações de metrô estão separadas por uma distância de m, qual é a velocidade máxima que o metrô pode alcançar entre as estações? (b) Qual é o tempo de percurso? (c) Se o metrô pára por em cada estação, qual é máxima velocidade escalar média do metrô de uma partida à próxima?
Passo 1
(a) O metrô precisa acelerar a partir do repouso até atingir a velocidade máxima, e então frear até parar na próxima estação, isso tudo enquanto percorre uma distância de .
Como a aceleração máxima é constante, o tempo de aceleração e de frenagem deve ser igual. Isso quer dizer que a velocidade máxima será atingida na metade do caminho:
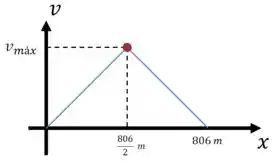
Passo 2
Beleza, então agora nosso problema é o seguinte: descobrir a velocidade de um corpo que parte do repouso com aceleração após andar .
Passo 3
(b) Agora vamos calcular o tempo total desse percurso. Como os tempos de aceleração e frenagem são iguais, só precisamos calcular um dos dois, e então dobrar o resultado.
Durante a aceleração, vimos que o corpo vai de até com aceleração , então:
Multiplicando por dois para incluir o tempo de frenagem, ficamos com o seguinte:
Passo 4
(c) Vamos lembrar da definição de velocidade escalar média:
Já vimos que o metrô demora para percorrer os entre as duas estações, então:
Se, além disso, ele gasta parado em uma estação antes de partir para a seguinte, a nova expressão para a velocidade será:
Resposta
(a) .
(b) .
(c) .