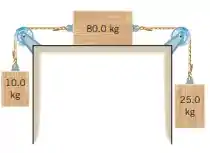
Os três diferentes objetos desenhados abaixo estão conectados por cordas e livres de atrito nas polias. Os objetos movem-se, e o coeficiente de atrito cinético entre o bloco do meio e a superfície é de 0,1. (a) Qual é a aceleração dos três objetos? (b) Encontre a tensão em cada uma das duas cordas.
Passo 1
Note que o balanço de forças em cada um desses blocos temos que:
A massa da direita tem uma diferença de tensão, , tentando puxar para baixo. De acordo com a segunda lei de Newton, temos então que:
Enquanto que o bloco do meio temos que:
Substituindo as equações primeira e segunda na terceira equação, temos que:
Passo 2
(b) Da parte (a), podemos tirar que:
Resposta
Ei, a resposta está no passo a passo :)