Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Termodinâmica Óptica- Ed: 2º - Capítulo 15.Exercícios e Problemas - Ex. 47

A água se encontra a uma profundidade d atrás de uma represa de largura w .

a. Obtenha uma expressão para a força resultante da água sobre a represa.

b. Calcule a força resultante sobre uma represa de 100 m de largura com profundidade de água de 60 m

Passo 1

a) Bom! Vamos fazer um esboço dessa represa...

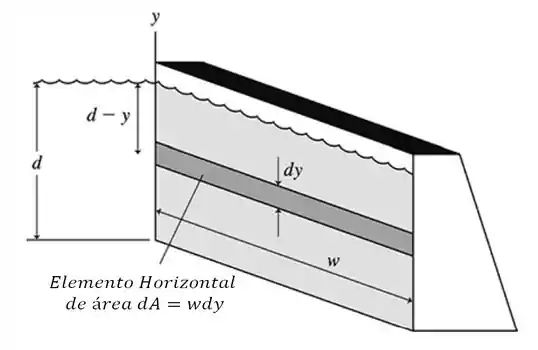
Vamos começar trabalhando com o diferencial em y ... Como podemos ver aí...

d A = w d y

Lembra lá qual a fórmula da pressão?

P = F A

F = P A

Derivando dos dois lados, obtemos que...

d F = P d A

Agora se liga! A medida que vamos aumentando a profundidade e nos distanciando da superfície da água lá no topo da represa, sujeita a pressão atmosférica de...

p a t m = 1,013 ⋅ 10 5   P a

Cê n concorda que dá pra a gente escrever essa pressão em função de y ... Desse jeito aqui;

P = ρ á g u a g ( d - y )

Passo 2

Pronto! Matamos a questão! Susbstituindo o P   e o d A que obtivemos na fórmula abaixo...

d F = P d A

E assim, obtemos a seguinte expressão...

d F = ρ á g u a g ( d - y ) w d y

Aí é só integrar em y ...

∫ d F = ∫ ρ á g u a g ( d - y ) w d y

Os limites de integração variam de 0 à F e de 0 até d ;

∫ 0 F d F = ∫ 0 d ρ á g u a g ( d - y ) w d y

F = ∫ 0 d ( ρ á g u a g d w - ρ á g u a g y w ) d y

F = ρ á g u a g d w y - ρ á g u a g y 2 2 0 d

F = ρ á g u a g w d 2 - ρ á g u a g w d 2 2

F = ρ á g u a g w d 2 2

Passo 3

b) Aí é só uma questão de substituir os valores numéricos pra achar o valor da força F ...

Sabendo que w = 100   m e d = 60   m , então...

F = 1000 ⋅ 9,8 ⋅ 100 ⋅ 60 2 2

F = 1,76 ⋅ 10 9   N

Resposta

a)

F = ρ á g u a g w d 2 2

b)

F = 1,76 ⋅ 10 9   N

Ver Outros Exercícios desse livro