Um aluno está descendo de skate uma rampa de 6,0 m de comprimento e inclinado em 18 em relação à horizontal. A velocidade inicial do skatista no topo da rampa é de 2,6 m/s. Negligencie o atrito e encontre a velocidade na parte inferior da rampa.

A velocidade do skatista na parte inferior da rampa pode ser encontrada resolvendo a equação cinemática para a velocidade

onde é a distância que o patinador se move descer a rampa.

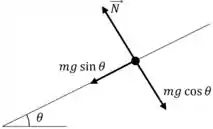
Fiz um diagrama de corpo livre pra gente entender melhor o que tá acontecendo com esse skatista radical.

A força resultante, que acelera o skatista na rampa, é o componente do peso que é paralelo à inclinação

Portanto, sabemos da segunda lei de Newton que a aceleração do skatista na rampa é

Então, a velocidade do skatista no começo da rampa é