Uma motocicleta de 292 kg está acelerando ao longo de uma rampa com uma inclinação de 30,0 acima da horizontal. A força de propulsão que empurra a motocicleta subindo a rampa é 3150 N, e a resistência do ar produz uma força de 250 N que se opõe ao movimento. Encontre a magnitude da motocicleta aceleração.

Fiz um diagrama de corpo livre pra gente visualizar melhor as forças atuando na motocicleta.

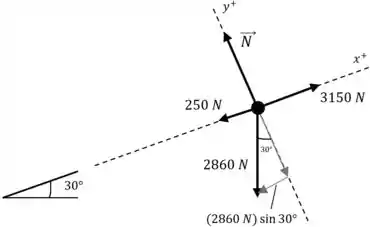
As forças que atuam na motocicleta são a força normal , a força de de propulsão, a força de da resistência do ar e o peso, que é .

Todas essas forças devem ser consideradas para determinar a força líquida para uso com a segunda lei de Newton para determinar a aceleração.

Em particular, notamos que o movimento ocorre ao longo da rampa e que tanto a propulsão quanto a resistência do ar são direcionadas paralelamente à superfície da rampa.

Em contraste, a força normal e o peso não agem paralelamente à rampa. A força normal é perpendicular a superfície da rampa, enquanto o peso atua verticalmente para baixo. No entanto, o peso tem um componente ao longo da rampa.

Ao desenhar o diagrama de corpo livre para a motocicleta, escolhemos o eixo para ser paralelo a superfície da rampa e para cima, a direção sendo perpendicular à superfície da rampa.

Já que a motocicleta acelera ao longo da rampa e buscamos apenas essa aceleração, podemos ignorar as forças ao longo do eixo (a força normal ( e o componente do peso). O componente da segunda lei de Newton é

Resolvendo para a aceleração