Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Oscilações, Ondas e Termodinâmica- Ed: 5º - Capítulo 17.Problemas - Ex. 49

Uma amostra de 4,00 L de um gás ideal diatômico com razão de calor específico de 1,40, confinado em um cilindro, realiza um ciclo fechado. O gás está inicialmente a 1,00 atm e 300 K. Primeiro, sua pressão é triplicada a volume constante. Então, expande-se adiabaticamente até sua pressão original. Finalmente, o gás é comprimido isobaricamente para seu volume original. (a) Trace um diagrama PV deste ciclo. (b) Determine o volume do gás ao final da expansão adiabática. (c) Encontre a temperatura do gás no início da expansão adiabática. (d) Encontre a temperatura ao final do ciclo. (e) Qual foi o trabalho resultante realizado sobre o gás para este ciclo?

Passo 1

Fala galera, ocêis tão baunzinho??

Bora láa

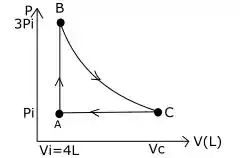
  1. Nesta questão, observemos que o gás expande em um processo isovolumétrico que leva do ponto A ao ponto B triplicando a sua pressão.

    2. Em seguida, expande em um processo adiabático do ponto B para o ponto C. Depois, retorna ao ponto A em um processo isobárico. Isso pode ser visto na Figura seguinte:

    Passo 2

  2. Notemos que, ao final da expansão adiabática (caminho BC), o gás possui volume V C .

    3. Sabendo que P B = 3 P A = 3 P i e que V B = V i = 4   L , Logo:

    P B V B y = P C V C y

    3 P i V i y = P i V C y

    V C y = 3 V i y

    V C = 3 1 y V i

    V C = 3 5 7 V i

    V C = 2,19 4,00   L

    V C = 8,77   L

    Passo 3

  3. Notemos que no inicio da expansão adiabática, o gás se encontra no ponto B, portanto teremos

    4. P B V B = n R T B = 3 P i V i = 3 n R T i

    T B = 3 T i = 3 300   K = 900 K

    Passo 4

  4. Assim, podemos ver que após o ciclo completo, o gás retorna ao estado inicial. Portanto:

    5. T A = T i = 300   K

    Passo 5

  5. Como o ciclo é fechado, a variação de energia interna é nula. Então, da primeira lei da termodinâmica, temos que:

W = - Q A B C A

Agora , no trecho AB, que ocorre a volume constante, a energia em forma de calor é:

Q A B = n C V ∆ V = n 5 2 R 3 T i - T i = 5 n R T i

Logo, no trecho BC, o processo é adiabático, então, Q B C = 0 .

Para o trecho CA, o processo ocorre a pressão constante, logo, temos

Q C A = n C P ∆ T

Portanto, precisamos obter ∆ T que é encontrado por:

P C V C = n R T C = P i 2,19 V i = 2,19   n R T i

Então

T C = 2,19   T i  

E também

Q C A = n C P ∆ T = n 7 2 R T i - 2,19 T i = - 4,17 n R T i

Passo 2

Logo, para o ciclo completo, temos :

Q A B C A = Q A B + Q B C + Q C A

Q A B C A = 5,00 - 4,17 n R T i = 0,829 n R T i

Da primeira lei da Termodinâmica e considerado que o caminho forma um ciclo fechado, temos então:

∆ E i n t ,   A B C A   = Q A B C A + W A B C A = 0

Portanto , o trabalho é dado por:

W A B C A = - Q A B C A = - 0,829 n R T i = - 0,829 P i V i

W A B C A = - 0,829 1,013 × 10 5   P a 4,00 × 10 - 3 m 3 = - 336   J

Resposta

Vide o passo a passo.

Ver Outros Exercícios desse livro