Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Oscilações, Ondas e Termodinâmica- Ed: 5º - Capítulo 17.Problemas - Ex. 83
Certo gás ideal tem calor específico molar de CV 5 7 2R. Uma amostra de 2,00 mols do gás sempre começa a pressão 1,00 3 105 Pa e temperatura de 300 K. Para cada um dos processos a seguir, determine (a) a pressão final, (b) o volume final, (c) a temperatura final, (d) a variação da energia interna do gás, (e) a energia adicionada ao gás por calor, e (f) o trabalho realizado sobre o gás. (i) O gás é aquecido a pressão constante a 400 K. (ii) O gás é aquecido a volume constante a 400 K. (iii) O gás é comprimido a temperatura constante a 1,20 3 105 Pa. (iv) O gás é comprimido adiabaticamente a 1,20 3 105 Pa
Passo 1
Fala galera, beleza? Bora resolver o nosso exercício? Vamos lá.
Vamos pegar aqui as informações que são dadas para a gente no enunciado:
Beleza, vamos começar calculando a pressão final. Como o gás é aquecido a uma pressão constante com temperatura de 400K, a pressão final permanece igual à inicial
Passo 2
Como estamos trabalhando com um gás ideal, para calcularmos o volume vamos usar
Show, temos o volume inicial já. Para calcularmos o final vamos usar:
No enunciado já é dado para a gente que , então
Passo 3
Beleza, agora vamos calcular a variação da energia interna do gás. Para isso:
E o interessante aqui galera é que esse também é o valor da energia adicionada ao gás pelo aquecimento
Como os valores são iguais, a gente consegue encontrar um resultado interessante pro trabalho feito:
Para calcularmos o volume de um gás ideal, vamos usar:
Além disso, para processos isotérmicos e adiabático:
Show, vamos dar uma olhada no gráfico do nosso problema
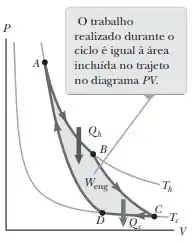
Vamos destacar aqui algumas informações
Beleza, vamos começar calculando o volume do ponto A:
Beleza, agora vamos calcular o volume do ponto C:
Beleza, agora vamos calcular o volume do ponto D:
Beleza, agora vamos calcular o volume do ponto B:
Resposta
Ei, a resposta está no passo a passo :)