Uma amostra de um gás ideal monoatômico está contida em um cilindro com um pistão. Seu estado é representado pelo ponto preto no diagrama PV mostrado na Figura PO18.9. Setas de A a E representam processos isobáricos, isotérmicos, adiabáticos e isovolumétricos pelos quais a amostra pode passar. Em cada processo, exceto D, o volume muda por um fator de 2. Todos os cinco processos são reversíveis. Classifique-os de acordo com a variação da entropia do gás do maior valor positivo para o maior valor negativo em módulo. Em sua classificação, mostre quaisquer casos de igualdade.
Passo 1
Fala galera, beleza? Bora resolver o nosso exercício? Vamos lá.
Bom, para começarmos, vamos trazer aqui o diagrama do exercício:
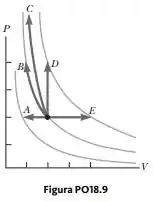
Como aqui temos uma amostra de gás ideal, a gente vai usar a equação:
Além disso, vamos usar a equação:
Show, agora vamos calcular para cada etapa do nosso diagrama, beleza? Então vamos começar.
Passo 2
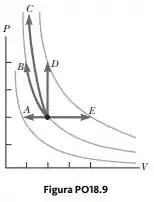
Vamos começar pelo processo A. Como aqui nós temos um processo isobárico, vamos usar:
Jogando na nossa fórmula da variação da entropia:
Show, agora que temos a nossa equação, nós vamos precisar integrar ela dos dois lados:
Beleza, como aqui a pressão é constante, o volume e a temperatura vão variar linearmente, mas inversamente proporcional. Como o enunciado nos diz que o volume muda por um fator de 2, podemos dizer que se o volume é dividido por 2, a temperatura é dobrada.
Vamos então dizer:
Passo 3
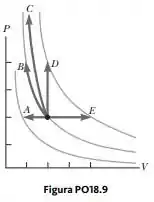
Agora vamos para o processo B. Como aqui nós temos um processo isotérmico, vamos usar:
Jogando na fórmula da variação da entropia vamos ter:
Beleza, agora vamos integrar de cada lado:
Assim como no Passo 1, faremos para o volume a mesma ideia da temperatura:
Passo 4
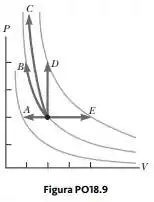
Agora vamos para o processo C. Como aqui nós temos um processo adiabático, vamos dizer que:
Jogando na fórmula da variação da entropia vamos ter:
Passo 5
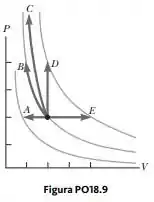
Agora vamos para o processo D. Como aqui nós temos um processo isovolumétrico, vamos dizer que:
Jogando na fórmula da variação da entropia vamos ter:
Beleza, agora vamos integrar de cada lado:
Como temos aqui um volume constante, a pressão e a temperatura são diretamente proporcionais, então como a Pressão dobra pelo gráfico, podemos dizer que o volume também vai dobrar, logo:
Passo 6
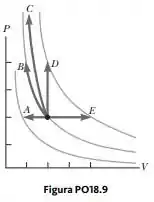
Agora vamos para o processo E. Como aqui nós temos um processo com pressão constante e o volume dobra, vamos dizer que:
Com isso podemos concluir que a variação da entropia se comporta: