Uma amostra de um gás ideal passa pelo processo mostrado na Figura P17.26. De A para B, o processo é adiabático; de B para C, é isobárico com 100 kJ de energia entrando no sistema por calor; de C para D, o processo é isotérmico; e de D para A, é isobárico com 150 kJ de energia saindo do sistema pelo calor. Determine a diferença em energia interna Eint,B - Eint,A.
Passo 1
Fala galera, beleza? Bora resolver o nosso exercício? Vamos lá.
Bom, aqui galera nós vamos usar a primeira lei da termodinâmica, aonde a variação da energia interna é calculada por:
Show, para entendermos como ela vai ser aplicada, vamos pegar aqui o gráfico do nosso exercício:
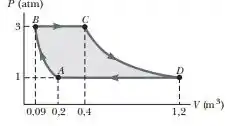
Como podemos ver, temos 4 etapas:
Então vamos ter que calcular e analisar cada etapa com calma. Bora!
Passo 2
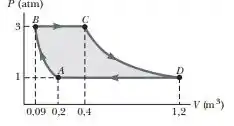
Vamos começar pela . Aqui temos um processo isovolumétrico, e pelo enunciado temos que a energia vai ser de
Com isso, o trabalho durante essa expansão vai ser:
A variação da energia interna vai ser:
Passo 3
Beleza, agora vamos olhar para a etapa . Como ela é isotérmica, podemos dizer que . Ou seja,
Ok, olhando para a etapa , pelo enunciado vamos ter .
Com isso, o trabalho será:
A variação da energia interna vai ser:
Passo 4
Ok, agora vamos pegar algumas informações aqui:
Logo:
Ok, além disso, vamos pegar:
Jogando na última fórmula: