Analise os estados ligados com funções de onda ímpar para o poço quadrado finito. Obtenha a equação transcendental para as energias permitidas e resolva-a graficamente. Examine os dois casos-limites. Há sempre um estado ligado ímpar?
Passo 1
Fala aí, tranquilo? Vamos nessa questão seguir a mesma linha do livro para encontrar os estados ligados de funções de onda ímpares. Assim, as soluções são do tipo:
Assim, vamos utilizar duas condições de contorno: a continuidade da função de onda e a continuidade da sua derivada em . Assim, vem:
E da derivada, temos:
Passo 2
Dividindo as duas equações, chegamos em:
Fazendo e , como o livro já fez para funções pares, ficamos com:
Essa equação transcendental pode ser analisada graficamente, assim como foi feito para funções pares. Os gráficos são do tipo:
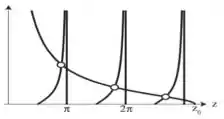
Passo 3
No limite em que é grande, as intersecções tendem a ocorrer próximos de , com par! Assim, nesse limite temos:
Já para o poço raso, se , não teremos nenhum estado ligado! Ou seja, se tivermos um potencial dado por:
Não teremos nenhum estado ligado relacionado às funções de onda ímpares.
Resposta
Se , não teremos nenhum estado ligado relacionado às funções de onda ímpares.