Enunciado
Física - Alonso e Finn - Campos e Ondas- Ed: 2º - Capítulo 14.Problemas - Ex. 68
Um anel de raio a carrega uma carga q. Calcule o potencial e o campo efetivo em pontos localizados no eixo perpendicular ao plano do anel.
Passo 1
Oiii tudo bem?
Vamos lá para mais um problema bem legal ein!
Passo 2
Vou desenhar pra gente entender melhor o problema, beleza?
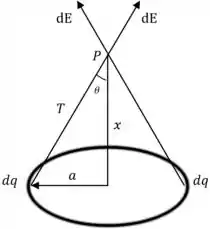
Passo 3
Temos que
Onde, nesse campo o ponto é
Substituindo na equação para
Passo 4
Aplicando integral dos dois lados da equação podemos encontrar