Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 75

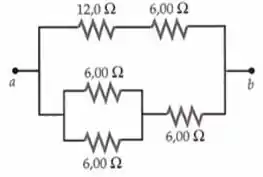
(a)Resistência a resistência equivalente entre os pontos a e b na Figura 26-56. (b) Se a queda de potencial entre os pontos a e b é 12   V , determine a corrente em cada resistor.

Passo 1

Eae galera! Tudo tranquilo? Dando uma olhada na questão, nós começaremos resolvendo a resistência equivalente em cada ramo. Para achar a corrente, usaremos a lei de Ohm.

Passo 2

Vamo lá. Calculando a R e q , vamos dividir pelo ramo de cima e pelo ramo de baixo para o nosso calculo de depois calcular o pararelo entre os dois. Para o ramo de cima:

R e q 1 = 12 + 6 = 18   Ω

R e q 2 = 6 | | 6 + 6 = 9   Ω

Agora calculando a resistência equivalente entre os dois ramos temos:

R e q = 18 | | 9 = 18 ⋅ 9 18 + 9 = 6   Ω

Passo 3

Agora calculando as correntes em cada resistor, vamos usar uma lei de ohm pra calcular a corrente que entra no circuito.

12 = 6 ⋅ I

I = 2   A

Quando chega no nó, a corrente vai para os dois ramos. E calculando a corrente em cada ramos temos:

Para o ramo de cima:

I = I 12 = I 6 = V a b R e q 3 = 12 18 = 667   m A

Para o ramo de baixo, no resistor de 6 Ohms:

I = I 6 = V a b R e q 2 = 12 9 = 1.33   A

Para cada resistor em pararelo no ramo de baixo, basta dividir por 2 o valor que achamos acima, já que a corrente vai se dividir igualmente porque os resistores são iguais.

I 6 | | 6 = 1.33 A 2 = 667   m A

Fechou? Então é isso! Até próxima galera!

Resposta

a )   R e q = 6   Ω

b )   I 12 = I 6 = 667   m A

I 6 b a i x o = 1.33   A

I 6 | | 6 = 667   m A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 29-25, R 1=20,0 Ω ,R 2=10,0 Ω O e a força eletromotriz da fonte ideal é E= 120 V. Determine a corrente no ponto a (a) com apenas a chave S1 fechada; (b) com apenas as chaves S1 e S2 fechadas;
A Fig. 29-26 mostra três resistores de 20,0 Ω . Determine a resistência equivalente (a) entre os pontos A e B; (b) entre os pontos A e C; (c) entre os pontos B e C.
Duas lâmpadas, uma de resistência R1, e a outra de resistência R2, R 1R 2 , são ligadas a uma bateria (a) em paralelo e (b) em série. Qual lâmpada é mais brilhante em cada caso?
Na Fig. 29-8 determine a diferença de potencial V d-V c entre os pontos d e c se E1 = 4,0 V, E2 = 1,0 V, R 1 ,=R 2=10 Ω , R3 = 5,0 Ω e a fonte é ideal.
Uma linha de força de 120 V é protegida por um fusível de 15 A. Qual é o número máximo de lâmpadas de 500 W que podem operar, simultaneamente, em paralelo, nessa linha sem “queimar” o fusível?