Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Problemas - Ex. 50
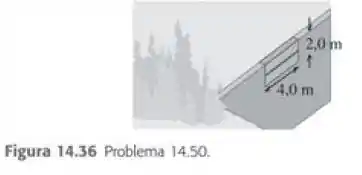
A aresta superior da comporta de uma represa está em contato com a superfície da água. A comporta tem 2,0 m de altura, 4,0 m de largura e uma articulação ao longo de uma linha horizontal passando pelo seu centro (Figura 14.26). Calcule o torque produzida pela força da água em relação ao eixo da articulação. (Sugestão: Use uma procedimento análogo ao adotado no problema 14.49; calcule o torque sobre uma estreita faixa horizontal situada a uma profundidade h e integre sobre a comporta.)
Passo 1
Vamos usar a equação para encontrar a pressão do manômetro versus a profundidade, e a equação para relacionar a pressão com a força.
Em uma faixa do portão, calcularemos o torque como força vezes o momento do braço e seguir o procedimento descrito na dica para calcular o torque total.
Seja o torque devido à força útil da água na metade superior do portão, seja o torque devido à força sobre metade inferior para calcular o torque total.
Com a convenção de sinalização indicada, é positivo e é negativo; portanto, o torque líquido sobre a dobradiça é
Seja H a altura do portão.
Passo 2
Na metade superior do portão:
Vamos calcular o torque devido à força em uma faixa estreita de altura localizada a uma distância abaixo da parte superior do portão
Em seguida, vamos integrar para obter o torque total.
Passo 3
A força total na tira é , onde é a pressão nessa profundidade e
com
O momento do braço é
Então
Passo 4
Metade inferior do portão:
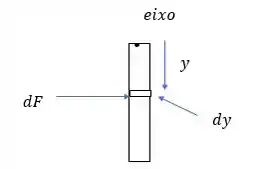
Considere a faixa estreita mostrada na ultima Figura, a profundidade da faixa é
então a força é
Passo 5
O momento do braço é , então
Passo 6
Então
As forças e torques nas metades superior e inferior do portão estão em direções opostas.
o valor líquido subtraindo as magnitudes. O torque na metade inferior é maior que o torque na metade superior já que a pressão aumenta com a profundidade.