Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Problemas - Ex. 73

Uma barra de aluminio é completamente recoberta por uma camada de ouro formando um lingote com peso igual a 45,0 N. Quando você suspende o lingote em uma balança de mola e a seguir o mergulha na água, a leitura da balança indica 39,0 N. Qual é o peso do ouro na camada?

Passo 1

E aí galera, aqui aplicaremos a segunda lei de Newton ao lingote. Usaremos a expressão para a força de flutuação dada pelo princípio de Arquimedes para resolver o volume do lingote. Em seguida, usaremos os fatos de que a massa total é a massa do ouro mais a massa do alumínio e que o volume do lingote é o volume do ouro mais o volume do alumínio.

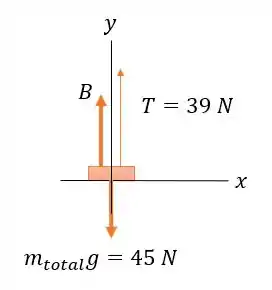
Passo 2

Então, aplicando a segunda lei de Newton descobriremos B

∑ F y = m a y

B + T - m t o t a l g = 0

B = m t o t a l g - T

B = 45   N - 39   N = 6   N

Também

m t o t a l g = 45   N

Então

m t o t a l = 45 N 9,8 m / s 2 = 4,59   k g  

Podemos usar o valor conhecido da força flutuante para calcular o volume do objeto:

B = ρ w V o b j g = 6   N

Assim,

V o b j = 6 N ρ w g = 6 N ( 1000 k g / m 3 ) ( 9,8 m / s 2 ) = 6,122 × 10 - 4   m 3

Passo 3

Sabemos duas coisas:

  1. A massa m o do ouro mais a massa a m a do alumínio deve adicionar a m t o t a l :

    2. m o + m a = m t o t a l

    Escrevemos isso em termos dos volumes V o do ouro e V a do alumínio:

    ρ o + V o + ρ a + V a = m t o t a l

  2. Os volumes V a e V o devem adicionar para fornecer V o b j :

V o b j = V a + V o

Isso implica que

V a = V o b j - V o

Vamos utilizar isso na equando em (1) para eliminar V a :

ρ o V o + ρ a V o b j - V o = m t o t a l

Logo,

V o = m t o t a l - ρ a V o b j ρ o - ρ a = 4,59   k g - ( 2,7 × 10 3 k g / m 3 ) ( 6,122 × 10 - 4   m 3 ) 19,3 × 10 3 k g / m 3 - 2,7 × 10 3 k g / m 3 = 1,769 × 10 - 4   m 3

Então,

m o = ρ o V o = 19,3 × k g m 3 1,769 × 10 - 4   m 3 = 3,41   k g

E o peso do ouro é

p e s o o = m o g = 33,4   N

O ouro é 29 % do volume, mas 74 % da massa, uma vez que a densidade do ouro é muito maior do que a densidade do alumínio.

Resposta

33,4   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura, um bloco retangular é gradualmente empurrado para dentro de um líquido. O bloco tem uma altura d ; a área das faces superior e inferior é A=5,67c m ² ² . A Fig. 14-39b mostra o peso aparent
Um flutuador tem a forma de um cilindro reto,com 0,5m de altura e 4,0m ² ² de área das bases; sua massa específica é 0,4 vezes a massa específica da água doce. Inicialmente o flutuador é mantido total
Na Fig 14-38, um cubo de aresta L=0,600m e 450k g de massa é suspenso por uma corda em um tanque aberto que contém um líquido de massa específica 1030k g / m ³ ³. Determine (a) o módulo da força total
Uma pequena esfera totalmente imersa em um líquido é liberada a partir do repouso e sua energia cinética é medida depois que se desloca 4,0c m no líquido. O gráfico mostra os resultados depois de muit