Uma arma é colocada na base de uma colina, cuja inclinação com a horizontal é . Se a arma está inclinada em um ângulo com a horizontal, e a velocidade de disparo é , calcule a distância, medida ao longo da colina, da arma ao ponto de queda do projétil.
Passo 1
Esse é um problema sobre lançamento oblíquo. O primeiro passo é fazer um desenho da situação:
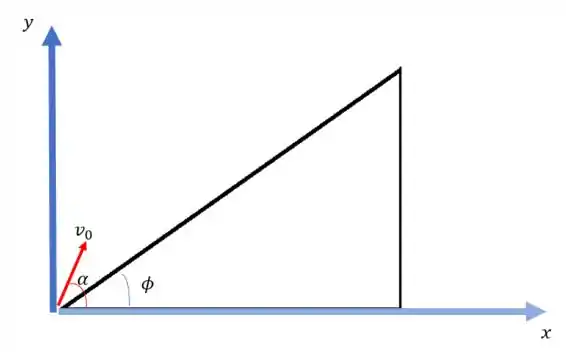
O projétil é lançado da base da colina (plano inclinado) com uma velocidade e fazendo um ângulo com o eixo . A inclinação do plano inclinado é .
O segredo para resolver esse problema é escrever a posição do projétil como função de ao longo da trajetória parabólica. Para isso, começamos decompondo o vetor velocidade inicial:
Passo 2
Na direção vertical, temos um movimento uniformemente acelerado com aceleração para baixo:
Como , e , temos que
Já na horizontal, temos um movimento uniforme:
Como :
Daí, substituímos na equação para :
Portanto,
A seguir representamos essa trajetória parabólica:
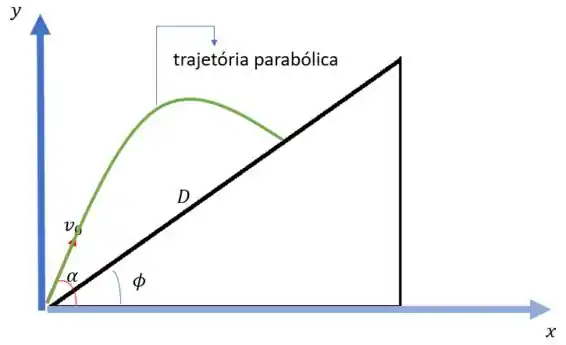
Passo 3
Agora só falta achar a distância ao longo do plano inclinado. Para isso, vamos procurar o ponto em que o projétil atinge o plano inclinado, cuja equação de reta é
Daí, basta igualar a equação da parábola com a equação da reta:
Simplificando de todos os termos, achamos
Portanto,
A distância é
Como , temos que
Substituindo a expressão para :