Um avião voa horizontalmente na altitude com velocidade . No instante em que está verticalmente acima de um canhão antiaéreo, ele é atingido. Calcule a velocidade mínima e o ângulo de disparo do projétil, para que um avião seja atingido nessas circunstâncias.
Passo 1
O enunciado é um pouco estranho. Se o avião é atingido exatamente no instante em que ele está verticalmente acima do canhão, isso significa que o tiro deve ser dado verticalmente de modo que
A seguir fazemos um esboço da situação:
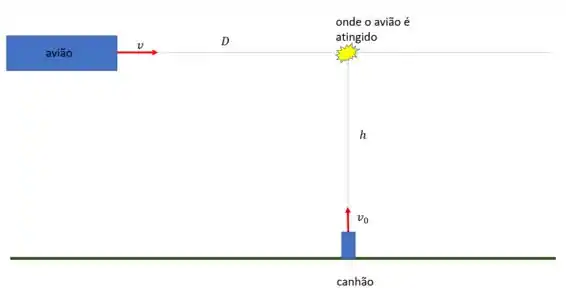
O problema seria muito mais interessante se o enunciado tivesse dito “No instante em que está verticalmente acima de um canhão antiaéreo, o projétil é atirado”. Nesse caso, o movimento do projétil seria parabólico com sua velocidade horizontal sendo igual a velocidade do avião e o ângulo obviamente não seria . Todavia, vamos seguir o que o enunciado nos disse, mesmo sendo um pouco esquisito...
Passo 2
Para achar a velocidade mínima , precisamos garantir que o projétil ao menos chegue na altura . Para isso, vamos supor que ele chega nessa posição com velocidade nula:
Esse é o máximo de informação que conseguimos tirar da situação descrita no enunciado...