Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Oscilações, Ondas e Termodinâmica- Ed: 5º - Capítulo 14.Problemas - Ex. 18

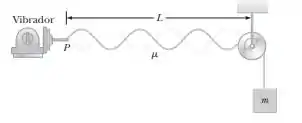
No arranjo mostrado na Figura P14.18, um corpo pode ser pendurado em uma corda (com densidade de massa linear μ = 0,00200   k g / m ) que passa sobre uma roldana leve. A corda é conectada a um vibrador (de frequência constante f ), e o comprimento da corda entre o ponto P e a roldana é L = 2,00 m. Quando a massa m do corpo é 16,0 kg ou 25,0 kg, ondas estacionárias são observadas; no entanto, não se observam ondas estacionárias com nenhuma massa entre esses valores. (a) Qual é a frequência do vibrador? Observação: quanto maior a tensão na corda, menor o número de nodos na onda estacionária. (b) Qual é a maior massa do corpo para a qual ondas estacionárias poderiam ser observadas?

Passo 1

Falaaa galerinhaaa, tudo na boaa??

Bora lá??

Esquematicamente teremos a seguinte situação:

A velocidade de propagação de uma onda em uma corda é dada pela seguinte equação:

v = T μ

Em que T representa a tensão e μ a densidade linear da corda. Vamos desenhar o D.C.L de massa:

T - m g = 0

T = m g

Vamos relembrar que ondas estacionarias ocorrem para os seguintes comprimentos de corda:

λ = 2 L n ,     n = 1 ,   2 ,   3 , …

Como v = λ f teremos o seguinte:

λ f = T μ = m g μ

Finalmente:

2 L n f = m g μ

Passo 2

  1. O enunciado informa que nenhuma massa entre m 1     e     m 2 é capaz de produzir ondas estacionárias. Logo, temos que:

    2. 2 L n f = m 1 g μ

    Em que

    2 L n f = m 2 g μ

    Podemos dividir as duas equações anteriores para tomar conhecidos os valores de n e de n - 1 .

    Então

    2 L n f 2 L n - 1 f = m 1 g μ m 2 g μ

    Logo:

    n - 1 n = m 1 m 2

    n - 1 n 2 = m 1 m 2 = 16 5 = 4 5

    Passo 3

    Logo, temos que n - 1 = 4   e   n = 5 . Agora podemos calcular a frequência do vibrador para cada massa. Para m = 16   k g , temos:

    2 L 5 f = m 1 g μ

    f = 5 2 L m 1 g μ

    Então

    f = 5 4,00 16 ⋅ 9,8 0,00200

    f = 350   H z

    Para m = 25   k g ,   t e m o s :

    2 L 4 f = m 1 g μ

    f = 4 2 L m 1 g μ

    Então

    f = 4 4,00 25 ⋅ 9,8 0,00200

    f = 350   H z

    Passo 4

  2. Vamos manter em mente que:

2 L n f = m g μ

Para uma onda estacionária a massa será máxima m m á x quando tivemos n = 1 . Sendo assim:

2 L f = m m á x g μ

Logo:

m m á x = 4 L 2 f 2 μ g

m m á x = 4 2 2 350 2 0,002 9,8

m m á x ≅ 400   k g

Resposta

  1. 350   H z
  2. 400   k g
Ver Outros Exercícios desse livro