(a) Um aspirador de pó muito potente tem uma mangueira de 2,86 cm de diâmetro. Com a ponta da mangueira colocada perpendicularmente na face plana de um tijolo, qual é o peso do tijolo mais pesado que o aspirador é capaz de levantar? (b) E se? Um polvo usa uma ventosa de diâmetro 2,86 cm em cada uma das duas conchas de um molusco numa tentativa de abrir suas conchas. Encontre a maior força que o polvo pode exercer sobre um molusco em água
salgada a 32,3 m de profundidade.
Passo 1
Fala aí! A princípio, parece que o enunciado não nos dá informações suficientes, né? Mas olha só, quando ele fala sobre um aspirador de pó “muito potente”, vamos assumir que este tem um motor capaz de criar um vácuo perfeito em seu interior. Com isso, a força máxima é gerada quando toda a pressão atmosférica empurra o tijolo contra a mangueira.
Beleza, nós sabemos que a pressão é expressa pela força dividida pela área:
Também, podemos facilmente encontrar o valor da área, já que o enunciado nos informou a medida do diâmetro da mangueira. Além disso, a pressão aqui será a própria pressão atmosférica, que vale aproximadamente Assim, podemos substituir os valores e resolver para F:
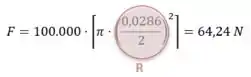
Passo 2
Para encontrar a força que o polvo deve exercer, o processo é bem similar. A diferença é que aqui devemos considerar não somente a pressão atmosférica, mas também a pressão da água salgada a uma profundidade de 32,3 metros. Lembre que podemos calcular essa pressão multiplicando a densidade, a gravidade e a profundidade (), então, a pressão total será:
A densidade da água salgada é aproximadamente 1.025 kg/m³. Vamos substituir os valores.
Com isso, podemos calcular a força exercida pela ventosa do polvo. Considerando que ela tenha a área de um círculo de diâmetro 2,86 cm, a conta será bem parecida com a que fizemos no passo anterior. Bora lá.