Enunciado
Física - Griffiths - Mecânica Quântica- Ed: 2º - Capítulo 2.Problemas - Ex. 47
Atenção: esse é um problema estritamente qualitativo, e nenhum cálculo será permitido! Considere o potencial do 'poço quadrado duplo' (Figura 2.21). Suponha que a profundidade V0, e a largura a são fixas, e amplas o suficiente para que vários estados ligados aconteçam.
(a) Esboce a função de onda do estado fundamental, e do primeiro estado excitado, (i) para o caso b= 0, (ii) para b a e (iii) para b>> a
(b) Qualitativamente, como as energias correspondentes (E, e E,) variam conforme b vai de 0? Esboce E, (b) e E, (b) no mesmo gráfico.
(c) O poço duplo é um modelo primitivo em uma dimensão para o potencial experimentado por um elétron em uma molécula diatômica (os dois poços representam a força atrativa dos núcleos). Se os núcleos estão livres para se mover, eles adotarão a configuração de energia mínima. Sob a perspectiva de suas conclusões em (b), o elétron tende a atrair os núcleos ou separá-los? (E claro que também devemos levar em conta a repulsão internuciear, porem. esse é um problema a parte.)
Passo 1
O enunciado pede para que não façamos cálculos. Assim, vamos entender cada caso.
Em a, nós temos para:
(i) b = 0, o que nos permite imaginar um poço quadrado finito ordinário. Além disso, tem a presença de decadência exponencial do lado de fora e o interior sinusoidal (cos para ψ1, sen para ψ2). Nenhum nó para ψ1, um nó para ψ2.
(ii) Para b=a, o estado fundamental é uniforme. Decadência exponencial fora, sinusoidal dentro dos poços, cosseno hiperbólico dentro de barreira. O primeiro estado excitado é ímpar - seno hiperbólico na barreira. Nenhum nó para ψ1, um nó para ψ2.
Assim, nós temos os seguintes gráficos:
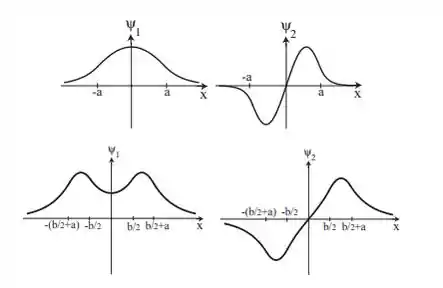
Passo 2
iii) Para b>>a, é muito parecido com (ii), mas a função de onda é muito pequena na região da barreira. Essencialmente dois finitos isolados nos poços quadrados; ψ1 e ψ2 são degenerados (em energia); eles são combinações lineares pares e ímpares dos estados fundamentais dos dois poços separados. Assim, teremos os seguintes gráficos:
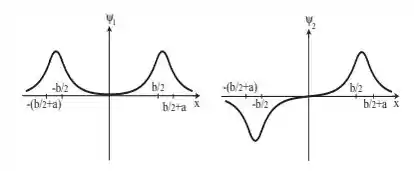
Passo 3
Em b, temos que b=0 e, pela equação 2.157 sabemos que as energias caem ligeiramente.
Nós temos as seguintes equações para estudar sobre as energias, para b=0:
E sabemos que
Para b>>a, a altura de cada poço isolado é igual a a, então
Dentro de cada poço, nós temos que Assim, quanto mais curvada a função de onda, maior a energia, o que prova o gráfico abaixo:
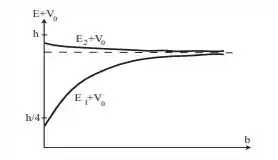
Como podemos ver, o gráfico acima condiz com tudo que explicamos até aqui!
Passo 4
Agora, em c, nós podemos dizer que no estado fundamental (par), a energia é mais baixa na configuração (i), com b → 0, então o elétron tende a unir os núcleos, promovendo a ligação dos átomos.
No primeiro estado excitado (ímpar), em contraste, o elétron separa os núcleos.
Resposta
Ei, a resposta está no passo a passo :)