Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.Problemas - Ex. 55
Um atleta com massa de está praticando exercícios de levantamento de peso. Saindo da posição de repouso, ele levanta, com aceleração constante, um haltere que pesa . Ele levanta o haltere a uma distância de em .
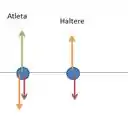
- Faça um diagrama de força do corpo livre para o haltere e outro para o atleta.
- Use os diagramas do item e as leis de Newton para achar a força total que os pés dele exercem sobre o solo enquanto ele ergue o haltere.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um atleta com massa de está praticando exercícios de levantamento de peso.
Saindo da posição de repouso, ele levanta, com aceleração constante, um haltere que pesa . Ele levanta o haltere a uma distância de em .
Queremos encontrar o diagrama de corpo livre do haltere e do atleta. Para isso, precisaremos analisar todas as forças em todas as direções dos corpos.
Com esses diagramas, poderemos encontrar a força total que os pés dele exercem sobre o solo enquanto ele ergue o haltere.
E aí? Vamos entender isso melhor?? 😉
Passo 2
No atleta estão agindo três forças: duas para baixo e uma para cima.
A força pra cima é a força que o chão faz sobre ele, como forma de reação à força que os pés do atleta fazem no chão.
Uma das forças para baixo é o peso sobre o atleta de e a outra é a força de levantamento do haltere, que puxa o corpo para baixo, enquanto o corpo empurra ele para cima.
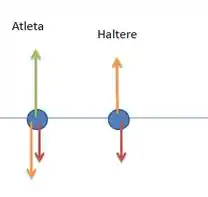No haltere agem apenas duas forças: a força peso (puxando ele para baixo) e a força de levantamento, para cima. O diagrama de forças do corpo livre é:
Em verde está representada a força do chão sobre o atleta, em vermelho o peso nos dois corpos e em laranja a força de levantamento que é vertical para cima no haltere e vertical para baixo no atleta.
Passo 3
Para descobrir a força do chão é preciso antes de tudo identificar a aceleração do sistema. Para isso o problema fornece os seguintes dados:
Onde é a velocidade inicial, é a altura final, é a altura inicial e é o tempo.
Vamos usar a equação horária da posição:
Substituindo os valores temos que a aceleração é:
Passo 4
Beleza? Agora sabendo a aceleração podemos aplicar a segunda lei de Newton para o haltere para descobrir a força de levantamento.
A massa do haltere é , daí usando o diagrama do haltere temos:
Mas não é essa força que o exercício pede? Não! É a que o chão faz no atleta! Mas precisávamos dessa força para aplicar a segunda lei no atleta, saca só:
ATENÇÃO AQUI! Quem está acelerando é o haltere e não o atleta! O atleta está em repouso! Então a força resultante sobre ele é zero!
Agora sim podemos encontrar Vamos lá?
Substituindo os valores teremos:
E sabendo da terceira lei que a força que o chão empurra o atleta é a mesma força que o atleta faz no chão, então a força que queremos vale .
Resposta
