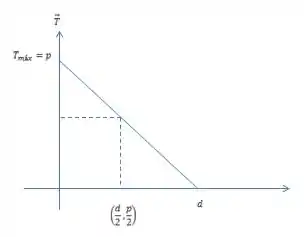
Um cabo uniforme fica pendurado verticalmente de cima para baixo, equilibrado por uma força de módulo de baixo para cima aplicada em sua extremidade superior. Qual é a tensão no cabo
- Em sua extremidade superior?
- Em sua extremidade inferior?
- Em seu ponto médio? Sua resposta para cada parte deve incluir um diagrama do corpo livre. (Sugestão: para cada questão, isole a seção ou o ponto do cabo que você analisará)
- Faça um gráfico da tensão na corda versus a distância a partir da extremidade superior.
Passo 1
No primeiro caso temos que levar em conta todo o peso do cabo, e a tensão no cabo vai ser igual ao peso. O diagrama de forças fica:
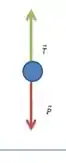
Passo 2
Sabemos que a força resultante no cabo é nula e a diferença de tensão na parte superior da parte inferior deve ser igual ao peso. Então, juntando isso com o resultado do item , temos que a tensão na parte inferior deve ser zero!
Passo 3
Repetindo nosso raciocínio, a força resultante deve ser zero. Então a diferença de tensão entre os pontos deve ser igual ao peso. Mas aqui estamos no ponto médio, então só precisamos levar em conta a metade inferior. Sendo assim a tensão no meio vai ser igual à metade do peso:
O diagrama de forças:
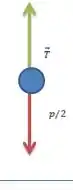
Passo 4
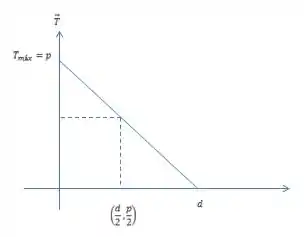
Resposta