Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 59
Na Áustria, havia um teleférico de rampa de esqui de 5,6 km. Uma gôndola do teleférico levava cerca de 60 min para percorrer esta distância. Se houvesse 12 gôndolas subindo, cada uma com urna carga de 550 kg de massa, e 12 gôndolas vazias descendo, e o ângulo de inclinação fosse de 30º, estime a potencia P da máquina necessária para operar o teleférico.
Passo 1
Olá, querido! Cê tá bem? Seguinte: temos essas gôndolas subindo e descendo o cabo do teleférico.
Ele quer saber a potência necessária da máquina que opera esse teleférico para fazer subir 12 gôndolas em cada uma com , levando no trajeto . (como ele não dá massa das gôndolas vazias, podemos desconsiderar as vazias que descem).
O esqueminha de uma gôndola vai ser esse:
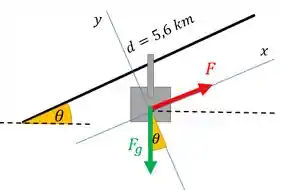
é a força necessária para fazer subir uma gôndola. Por isso ela está no sentido de fazer subir esse carrinho pelo cabo inclinado do teleférico.
A potência é dada pela razão entre o trabalho realizado pelo motor e o tempo que percorrido:
A ideia é a gente usar essa expressão para achar a potência do motor do teleférico. Bora!
Passo 2
O trabalho da força para mover a gôndola pelo cabo de comprimento vai ser dado pela fórmulinha:
Já que nossa e estão no mesmo sentido e é constante. Como temos gôndolas, o trabalho total que o motor do teleférico tem que realizar é
E assim, a potência total que esse motor deve ter vai ser:
Passo 3
Só falta a gente saber quem é para cada gôndola. Percebe que a gente colocou no nosso esqueminha na direção do movimento.
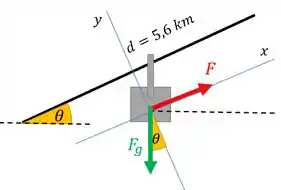
Aí o que a gente vai fazer é avaliar as forças que agem nessa direção para saber quando precisa valer , já que o trabalho é realizado nessa direção.
A gente quer que o carrinho se mova. Ele não precisa estar acelerado, só em movimento. Então a gente pode considerar que a velocidade dele é constante, e assim a aceleração em é nula, .
Aí aplicando a segunda lei de Newton:
Passo 4
Substituindo na expressão da potência:
Agora jogando os valores:
Passando o que tá em quilômetros para metros e o que tá em minutos para segundos: