Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 56

Use integração para determinar o momento de inércia de um disco fino uniforme de massa M e raio R em relação a um eixo do plano do disco que passa pelo seu centro. Confira sua resposta referindo à tabela 9-1.

Passo 1

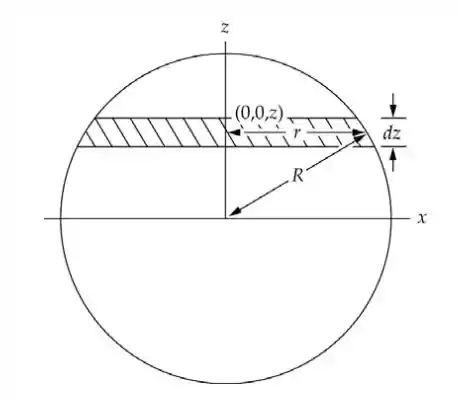
Seja x o eixo de rotação. O raio r da área marcada é igual a r = R 2 - z 2 , e sua massa d m é σ d A = σ 2 r d z = 2 σ R 2 - z 2 d z . Vamos integrar z 2 d m para determinar I, e dividir o resultado pela massa para eliminar os termos que não queremos.

Passo 2

I = ∫ z 2 d m = ∫ z 2 σ d A

I = ∫ - R R z 2 2 σ R 2 - z 2 d z

I = 2 σ ∫ - R R z 2 R 2 - z 2 d z

Vamos resolver a integral separadamente aqui embaixo. Fazendo x = R s e n θ , com θ no intervalo de - π 2 até π 2 , daí, R 2 - x 2 = R 2 cos 2 ⁡ θ e d x = R c o s θ d θ .

Não esquece de trocar os limites de integração!

Como a função é par, ∫ - R R z 2 R 2 - z 2 d z = 2 ∫ 0 R z 2 R 2 - z 2 d z .

S = 2 ∫ 0 π 2 R 2 s e n 2 θ R 2 cos 2 ⁡ θ d x = 2 ∫ 0 π 2 R 2 s e n 2 θ × R c o s θ × R c o s θ d θ

S = 2 R 4 ∫ 0 π 2 s e n 2 θ cos 2 ⁡ θ d θ = 2 R 4 ∫ 0 π 2 s e n 2 2 θ 4 d θ = R 4 2 ∫ 0 π 2 s e n 2 2 θ d θ

S = R 4 2 ∫ 0 π 2 1 - c o s 4 θ 2 d θ = R 4 4 ∫ 0 π 2 ( 1 - c o s 4 θ ) d θ

S = R 4 4 ( θ - s e n 4 θ 4 )

Substituindo θ = π 2 e θ = 0 , para terminar a integral definida:

S = 1 8 π R 4

Ufa, essa deu trabalho! Mas agora estamos tranquilos.

I = 2 σ ∫ - R R z 2 R 2 - z 2 d z

I = 2 σ 1 8 π R 4

I = σ π R 4 4

Passo 3

Mas a massa do disco é:

M = σ π R 2

Dividindo I por M, terminamos a questão obtendo:

I = 1 4 M R 2

Repara que essa é a expressão da tabela para um cilindro de comprimento L = 0 .

Resposta

I = 1 4 M R 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera com raio R 0,200 m tem densidade r que diminui com a distância r a partir do centro da esfera, de acordo com r 3,00 × 103 kg/m3 (9,00 × 103 kg/m4 )r. (a) Calcule a massa total da esfera. (b
Um disco uniforme possui raio R0 e massa M0. Seu momento de inércia para um eixo perpendicular ao plano do disco no centro do disco é 1 / 2M 0 R 0 2 . Você deverá dividir o momento de inércia do disco
Uma nova espécie de enguia foi descoberta, com a mesma massa, porém com um quarto do comprimento e o dobro do diâmetro da enguia americana. Qual é a relação entre seu momento de inércia em torno de se
Determine o momento de inércia de um cone maciço uniforme em relação a um eixo que passa através de seu centro (Figura P 9.90 ). O cone possui massa M e altura h . O raio do círculo de sua base é igua
Um ônibus de passageiro em Zurique, na Suíça, usa sua potência motora oriunda da energia acumulada em um volante grande. Utilizando-se de energia da rede elétrica, a roda é colocada em movimento perio