Um avião deve voar rumo norte, de para , e então voltar para . A distância entre e é . A velocidade do avião em relação ao ar é e a velocidade do vento é (a)Prove que o tempo para uma viagem de ida e volta, quando não há vento, , é . (b) Mostre que o tempo para uma viagem de ida e volta, quando o vento sopra para leste (ou oeste), é . (c) Mostre que o tempo para a viagem de ida e volta quando o vento sopra para o norte (ou sul) é (d) Qual é a possibilidade das viagens (b) ou (c) quando ? Para um dado valor de , qual tempo será o maior, ou ?
Passo 1
E aí, beleza?? Vamos resolver item por item esse problema. Inicialmente, para o item (a), consideremos:
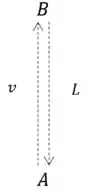
Nesse caso, o tempo de subida é idêntico ao tempo de descida. A distância percorrida é , assim, vem:
Passo 2
Agora, para o item (b), teremos uma composição de velocidades. Para que o avião se mantenha na direção vertical, a componente horizontal de deve anular , como segue a figura:
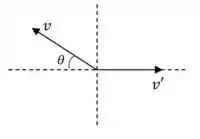
Assim, podemos encontrar a inclinação com:
Desse modo, a velocidade vertical fica:
Portanto, como a distância a ser percorrida continua sendo , vem:
Portanto:
Passo 3
Agora, para o item (c), como a velocidade do avião na ida e na volta são diferentes, devido à composição de velocidades:
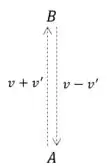
Assim, devemos considerar o tempo em cada trecho e, então, somá-los:
Ou seja:
Portanto:
Passo 4
No caso em que não é possível que o avião execute a trajetória desejada, pois, no caso do item (b), ele necessariamente se moveria em uma diagonal, enquanto no caso do item (c), o avião apenas conseguiria executar um dos trechos (na condição em que o vento sopra na direção favorável).
No caso em que, temos que , logo:
Dessa maneira, podemos escrever a seguinte relação:
Portanto:
Multiplicando por , chegamos em:
Ou seja:
Resposta
Ei, a resposta está no passo a passo :)