Um avião voa horizontalmente na altitude de l km com a velocidade de 200 . Ele deixa cair uma bomba sobre um navio que se move no mesmo sentido e com a velocidade de 20 . Prove que a bomba deve ser lançada quando a distância entre o avião e o navio é de 730 m. Resolva o mesmo problema para o caso ele o avião e o navio terem movimentos de sentidos contrários
Passo 1
Oiii tudo certo?
Vamos lá para mais um exercício?! Com certeza os engenheiros láaa a um tempão atrás estavam pensando nesse mesmo problema, só que para atacar em guerras de verdade. Então se prepara pra guerra e vamos resolver esse problema!

Passo 2
Fiz um desenho esquemático do que está acontecendo, pra gente visualizar melhor beleza? Sugiro que você faça isso para os problemas que for resolver, é sempre útil
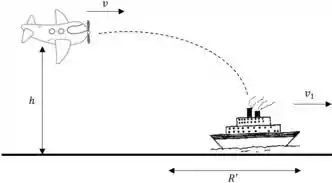
Passo 3
A bala vai cair no tempo
A altura é definida pela equação
Já que , podemos resolver a equação para
Passo 4
Neste tempo percorrerá uma distância , e temos uma relação básica e a distância é
Substituindo a relação para obtida anteriormente
Passo 5
Neste tempo percorrerá uma distância , e temos uma relação básica e a distância é
Passo 6
Para que a bomba encontre o navio, é necessário que a distância inicial entre o avião e o navio seja
Temos todos os dados para calcular essa distância
Então podemos substituir na equação
Passo 7
Para o caso de o avião e o navio terem movimentos de sentidos contrários, vamos fazer o mesmo procedimento. A diferença será que vamos considerar
Resposta
Ei, a resposta está no passo a passo :)