Um caçador mira um esquilo que está sobre um galho de árvore. No instante do disparo, o esquilo se solta do galho. Mostre que o esquilo não deveria ter se soltado, se pretendia continuar vivo.
Passo 1
Esse exercício é bem divertido. Imagine a seguinte situação: um atirador que não sabe física mira num esquilo. Como o atirador não sabe física, ele mira em linha reta no esquilo. Todavia, você deve saber que se o atirador fizer isso, ele vai errar o alvo, como mostrado na figura a seguir:
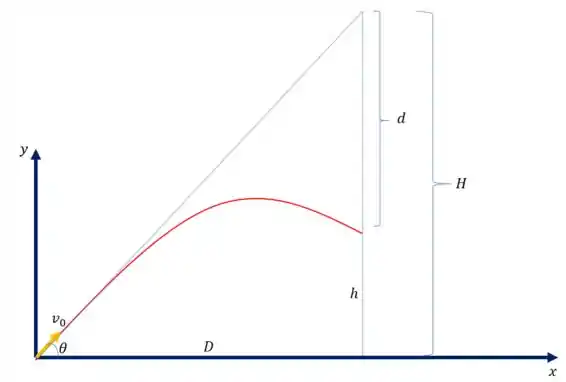
Vamos calcular a altura que o projétil vai atingir. Para isso, lembramos que a equação da trajetória parabólica é
Quando , temos , de modo que
Guarde essa informação!
Passo 2
Se o esquilo ficar paradinho no galho, o tiro não vai atingi-lo e ele vai sair vivo para contar a história para outro esquilinho. Agora, se no momento do tiro o esquilo se assustar e perder o equilíbrio, ele pode estar em apuros!
Vamos calcular a distância que o esquilo cai enquanto o projétil se movimenta. Para isso, lembramos que o tempo de voo do projétil é
Como , temos que
Para calcular a distância , usamos a fórmula de queda livre:
Substituindo o tempo de voo:
Aqui vem o pulo do gato! Observe que usando trigonometria em triângulos retângulo, podemos escrever
Assim,
Olhando na figura, vemos que a posição que o esquilo vai se localizar na queda coincide exatamente com a posição do projétil. Olha que coisa maluca: mesmo sem saber física e errando a mira, se o esquilo se assustar e cair no momento do tiro, ele será atingido!
Resposta
Demonstração.