Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Okuno - Física para Ciências Biológicas e Biomédicas- Ed: 1º - Capítulo Guia 1.8 - Ex. 25

Uma barra de massa M e comprimento L está fixada a parede por meio de uma dobradiça de massa desprezível, como ilustra a Figura G.1.13. A outra extremidade, que está sendo tracionada por uma corda com a forca   T → , amarra-se um bloco de massa m .

a. Esquematize todas as forças que agem sobre a barra.

b. Quais são os ângulos que as linhas de ação de cada forca formam com a horizontal?

c. Quais são os torques de cada forca em relação ao ponto O , localizado na dobradiça? Indique na figura.

Passo 1

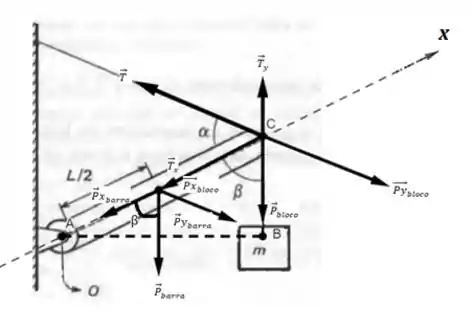
  1. Abaixo está o DCL, esquematizando todas as forças e seus respectivos pontos de ação:

    2. Passo 2

  2. Considerando o eixo x como passando pelo centro horizontal da barra: T → faz um ângulo α com a horizontal: P → b a r r a   faz um ângulo β com a horizontal: P → b l o c o   faz um ângulo β com horizontal

    3. Passo 3

  3. O ponto da dobradiça é ponto O : Vamos considerar positivo o sentido anti-horário:Se positivo o vetor está entrando no ponto e se negativo o vetor está saindo: Vamos analisar cada força:   T → : Vamos analisar ela em função de suas componentes x e y: T → x = T → ⋅ cos ⁡ α T → y = T → ⋅ sin ⁡ α Analisando o DCL, vemos que a força T → x não gera torque, pois sua linha de ação é coincidente ao ponto de rotação. Com isso apenas T → y   gera torque no ponto A :O momento gerado por T → y é dado por: τ A = T → ⋅ sin ⁡ α ⋅ O B -     Onde: Vamos achar a distância O B - em função do comprimento L da barra e dos ângulos α   e   β fornecidos pelo exercício:Usando o triângulo retângulo Δ O B C como referência, temos que sua hipotenusa é o comprimento da barra, usando as relações trigonométricas no triângulo retângulo, vamos determinar as distâncias. O B - L = sin ⁡ β   ⟹       O B - = L sin ⁡ β Subst. na expressão acima: τ O = T → ⋅ sin ⁡ α ⋅ L ⋅ sin ⁡ β ∴ τ O = T → ⋅ L ⋅ sin ⁡ α sin ⁡ β A força   T → y gera uma ação no sentido anti-horário na barra, portanto τ O positivo: ⊙

Passo 2

Vamos calcular o torque que o peso P → b l o c o gera no ponto O em função de suas componentes.Igualmente a força T → apenas a componente P → y b l o c o   gera torque no ponto, pelo mesmo motivo que citado no passo 3:

P → y b l o c o = P → b l o c o ⋅ sin ⁡ β

A distância perpendicular a sua linha de ação é   O B - : τ O b l o c o = P → b l o c o ⋅ sin ⁡ β ⋅ O B -   ⟹     τ O b a r r a = m ⋅ g ⋅ sin ⁡ β ⋅ L ⋅ sin ⁡ β

∴ τ O b l o c o = m ⋅ g ⋅ L ⋅ sin 2 ⁡ β  

A força   P → y b l o c o gera uma ação no sentido horário na barra, portanto τ O negativo: ⊕

Passo 3

Vamos calcular o torque que o peso P → b a r r a gera no ponto O em função de suas componentes.Igualmente a força T → e P b l o c o , apenas a componente P → y b a r r a   gera torque no ponto O, pelo mesmo motivo que citado no passo 3:

P → y b a r r a = P → b a r r a ⋅ sin ⁡ β

A distância perpendicular a sua linha de ação é   O B - 2 : τ O b a r r a = P → b a r r a ⋅ sin ⁡ β ⋅ O B - 2   ⟹     τ O b a r r a = M ⋅ g ⋅ sin ⁡ β ⋅ L 2 ⋅ sin ⁡ β

∴ τ O b l o c o = 1 2 ⋅ M ⋅ g ⋅ L ⋅ sin 2 ⁡ β  

A força   P → b a r r a gera uma ação sentido horário na barra, portanto τ O negativo: ⊕

Passo 4

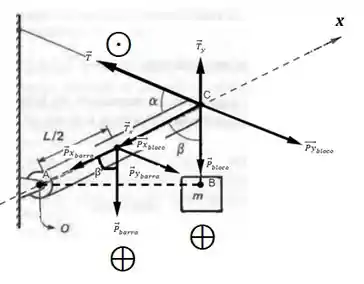
Figura representando as forças e o sinal de representação entrando ou saindo do ponto O:

Resposta

  1. DCL passo 1:
  2. T → faz um ângulo α com a horizontal: P → b a r r a   faz um ângulo β com a horizontal: P → b l o c o   faz um ângulo β com horizontal
  3. Torque gerado pela força T → : τ O = m ⋅ g ⋅ L ⋅ sin 2 ⁡ β   Torque gerado pelo peso do bloco P → b l o c o : τ O = m ⋅ g ⋅ L ⋅ sin ⁡ β Torque gerado pelo peso da barra P → b a r r a : τ O = 1 2 ⋅ M ⋅ g ⋅ L ⋅ sin 2 ⁡ β
Ver Outros Exercícios desse livro