Quais são os torques exercidos por uma esfera de ao ser segura por uma pessoa com o braço esticado na horizontal, em relação a um eixo que passa pelo:
- pulso;
- cotovelo;
- Ombro
Passo 1
Observe a ilustração, o ponto de giro está localizado no ponto :
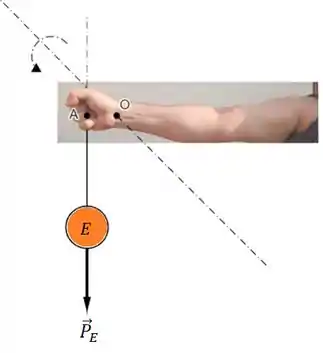
Passo 2
Agora vamos analisar as definições de torque ou momento: Obs.: Torque = Momento
Uma força gera torque ou momento num ponto , se a linha de ação da força for perpendicular ao eixo de rotação que passa pelo ponto :
Onde se adota de forma arbitrária, se positivo é o sentido horário ou anti-horário, porém a maioria das literaturas adotam como torque positivo o sentido anti-horário.
Onde:
Torque Força de ação Distância perpendicular a linha de ação da força:
Passo 3
Para o exercício em questão:
O torque resultante é dado pelo peso da esfera multiplicado pela distância :Adotando o sentido anti-horário como torque positivo:
Vamos aplicar as condições e definir o torque:
Passo 4
Como
Adotando
Massa da esfera foi fornecido:
Faremos o mesmo nos itens b e c:
b) Cotovelo
Passo 5
Observe a ilustração, o ponto de giro agora está localizado no ponto :
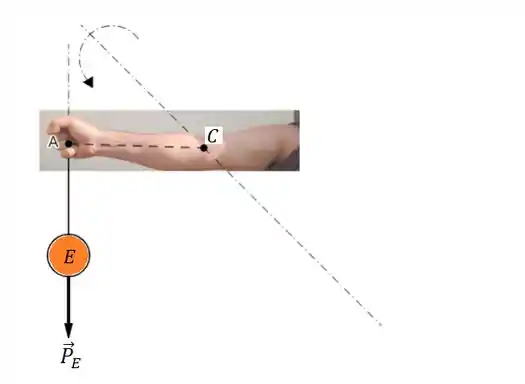
Passo 6
Semelhante ao item a, aplicando as propriedades de torque temos:
Usando os dados do item a, ficamos assim:
Massa da esfera foi fornecido:
c. ombro;
Passo 7
Observe a ilustração, o ponto de giro agora é o ponto :
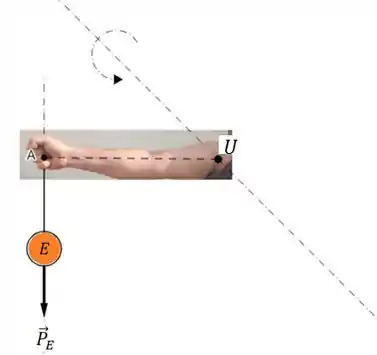
Passo 8
O que se pode concluir, analisando todos os itens calculados, é que, o torque é diretamente proporcional à distância do ponto de giro:
Resposta
- No pulso:
- No cotovelo:
- No ombro: