Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 74
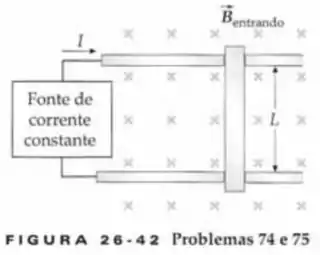
Uma barra metálica de massa desliza em um par de longos trilhos horizontais condutores, paralelos, separados por uma distância e conectados a um dispositivo que fornece corrente constante para o circuito, conforme mostrado na Figura 26-42. O circuito está em uma região com um campo magnético uniforme cuja direção é verticalmente para baixo. Não há atrito e a barra parte do repouso em .
Em que sentido a barra começará a se mover?
Mostre que no instante a barra terá uma rapidez de .
Passo 1
E aí bonit@s, como vocês estão? Preparados pra mais uma questão bacana?
Pois bem, para essa questão nós podemos usar uma equação de aceleração constante para relacionar a velocidade da barra transversal à sua aceleração e a segunda lei de Newton para expressar a aceleração da barra transversal em termos da força magnética agindo sobre ela. Podemos determinar a direção do movimento da barra transversal usando uma regra da mão direita ou, de forma equivalente, aplicando .
Passo 2
Se liga só que o primeiro item é resolvido somente com teoria e é bem simples: Como a força magnética está para a direita e a barra transversal começa do repouso, o movimento da barra transversal também será para a direita.
Passo 3
Para finalizar esse problema vamos começar usando uma equação de aceleração constante, expresse a velocidade da barra como uma função de sua aceleração e o tempo que ela esteve em movimento:
Como tivemos , podemos fazer
Utilizando a segunda lei de Newton temos que
Onde é a magnitude da força magnética agindo na direção do movimento transversal da barra, dada por
Dessa forma, para finalizarmos o problema basta substituirmos e de movo que obteremos
Pronto, está finalizado o nosso problema.
Resposta
Como a força magnética está para a direita e a barra transversal começa do repouso, o movimento da barra transversal também será para a direita