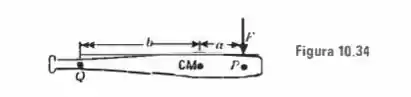
Um bastão de comprimento L e massa m repousa sobre um plano horizontal sem atrito (fig. 10.34). Durante o curto intervalo de tempo delta t, o bastão é atingido por uma força P que produz um impulso! A força age num ponto P situado a uma distância a do centro de massa. Procure (a) a velocidade do centro ele massa. e (b) a velocidade angular em torno do centro de massa, (c) Determine o ponto Q, que permanece inicialmente em repouso no referencial de laboratório, mostrando que b = !(l/a, onde K é o raio de giração em torno do centro de massa. O ponto Q é chamado centro de percussão. (Por exemplo, um jogador de basebol deve segurar o taco pelo centro ele percussão no sentido de evitar a desagradável sensação da reação do taco quando ele atinge a bola.) Prove também que, se a força for aplicada em Q, o centro ele percussão estará em P.
Passo 1
Faala galera!! Temos que, a equação da variação de momento é:
Como p0 estã no plano, então é nulo. Assim:
Passo 2
Sabemos que o momento angular em relação ao centro de massa é dado por:
, além de que:
, o torque externo em relação ao centro de massa.
Assim, encontramos w:
Passo 3
Aqui, teremos que encontrar o ponto Q.
e sempre se cumpre a condição de que
Resposta
Ei, a resposta está no passo a passo :)