Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 23.1 - Ex. 52

Um bastão de comprimento L tem carga total Q distribuída uniformemente ao longo do seu comprimento. O bastão está ao longo do eixo y com uma extremidade na origem. (a) Determine uma expressão para o potencial elétrico como uma função da posição ao longo do eixo x . (b) Mostre que o resultado obtido na parte (a) se reduz a V = k Q / x para x ≫ L . Explique por que este resultado é esperado.

Passo 1

Fala ai galera, tranquilo? A figura abaixo representa, de maneira esquemática, o enunciado:

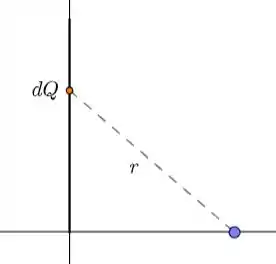
Para calcular o potencial elétrico do fio, inicialmente dividimos o fio em várias cargas puntiformes d Q . O potencial de cada uma dessas cargas valerá:

d V = k d Q r

Para obter o potencial inteiro, realizamos a integração,

V = k   ∫ d Q r

Passo 2

  1. Temos que d Q = Q L   d y e r = x 2 + y 2 . Assim,

    2. V = k Q L ∫ 0 L d y x 2 + y 2

    Usando uma tabela de integrais, temos que

    V = k Q L ln ⁡ L + x 2 + L 2 x

  2. Podemos escrever o potencial como

V = k Q L ln ⁡ L x + 1 + L 2 x 2

Como x ≫ L , então 1 + L 2 x 2 1 / 2 ≈ 1 + L 2 2 x 2 (pois 1 + θ n ≈ 1 + n θ para θ ≪ 1 ). Dessa forma, temos que

V = k Q L ln ⁡ L x + 1 + L 2 2 x 2

Porém, L 2 2 x 2 ≪ L x de modo que podemos desprezar esse fator. Segue que

V = k Q L ln ⁡ 1 + L x

Além disso, temos que ln ⁡ 1 + θ ≈ θ para θ ≪ 1 . Dessa maneira, temos

V ≈ k Q L ⋅ L x = k Q x

que é o que queríamos demonstrar!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O potencial elétrico V no espaço entre as placas de um determinado, e hoje em dia obsoleto, tubo a vácuo é dado por V = 1530V / m 2 x 2 , onde x é a distância a partir de uma das placas. Calcule a int
A que distância ao longo do eixo de um disco uniformemente carregado de raio R o seu potencial elétrico é igual à metade do yalor do potencial sobre a superfície do disco em seu centro?
Considere a carga pontual com q = 1,5 × 10 - 8 C . (a) Qual o raio de uma superfície eqüipotencial tendo um potencial de 30 V? Suponha que V = 0 no infinito. (b) As superfícies cujos potenciais difere
Movendo-se de A para B ao longo das linhas de campo elétrico, o campo elétrico realiza 3,94 × 10 - 19J de trabalho sobre um elétron no campo ilustrado na Fig.. Quais são as diferenças no potencial elé
Uma carga elétrica de - 9,12 n C está uniformemente distribuída ao redor de um anel de raio 1,48m que se encontra no plano y z com seu centro na origem. Uma partícula com carga de - 5,93 pC é posicion