Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 23.1 - Ex. 51

Um bastão de comprimento L tem carga total Q distribuída uniformemente ao longo de seu comprimento. O bastão está ao longo do eixo y com seu centro na origem. (a) Determine uma expressão para o potencial elétrico como uma função da posição ao longo do eixo x . (b) Mostre que o resultado obtido na parte (a) se reduz a V = k Q / x para x ≫ L . Explique por que este resultado é esperado.

Passo 1

Fala ai, galera, tranquilo? Veja o esquema a seguir que representa o enunciado:

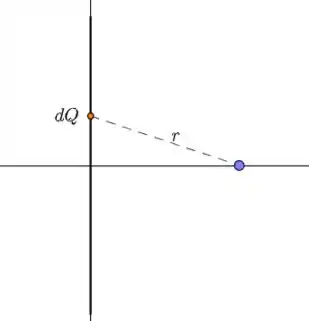
Queremos calcular o potencial elétrico do fio. Para isso, vamos dividir o fio em pequenas cargas d Q , de modo que o potencial elétrico dessa pequena carga será:

d V = k d Q r

O potencial total será obtido fazendo a integração:

V = k   ∫ d Q r

Passo 2

  1. Notemos que d Q = Q L d y e r = y 2 + x 2 . Logo, temos que

    2. V = k Q L ∫ - L / 2 L / 2 d y y 2 + x 2

    Usando uma tabela de integrais, temos que

    V = k Q L ln ⁡ x 2 + 1 4 L 2 + 1 2 L x 2 + 1 4 L 2 - 1 2 L

  2. Agora, vamos supor que x ≫ L . Assim, x 2 ≫ 1 4 L 2 , de modo que x 2 + 1 4 L 2 = x 1 + L 2 4 x 2 ≈ x 1 + L 2 8 x 2 onde usamos 1 + θ n ≈ 1 + n θ para θ ≪ 1 . Assim, temos

V = k Q L ln ⁡ 1 + L 2 4 x 2 + L 2 x 1 + L 2 4 x 2 - L 2 x ≈ k Q L ln ⁡ 1 + L 2 8 x 2 + L 2 x 1 + L 2 8 x 2 - L 2 x

Porém, L 2 8 x 2 ≪ L 2 x de modo que podemos ignorá-lo. Sendo assim,

V ≈ k Q L ln ⁡ 1 + L 2 x 1 - L 2 x = k Q L ln ⁡ 1 + L 2 x - ln ⁡ 1 - L 2 x

Como ln ⁡ 1 + θ ≈ θ para θ ≪ 1 , segue que

V ≈ k Q L L 2 x - - L 2 x = k Q L L x = k Q x

que é o queríamos provar!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o gradiente do potencial radial, ∂ V / ∂ r , sobre a superfície de um núcleo de ouro. Veja o Problema Resolvido 28-7.
O Exercício 39 do Cap. 26 trata do cálculo de Rutherford de um campo elétrico a uma distância r do centro de um átomo. É também dado o potencial elétrico como V = Z e 4 π ϵ 10 1 r - 3 2 R + r 2 2 R 3
Na Fig. 28-39 esboce qualitativamente ( a ) as linhas de campo elétrico e ( b ) as interseções das superfícies eqüipotenciais com o plano da figura. (Sugestão: Considere o comportamento da região próx
Duas linhas de cargas são paralelas ao eixo z. Uma, de carga por unidade de comprimento + λ , está a uma distância a do lado direito deste eixo. A outra, de carga por unidade de comprimento - λ , está
Considere que o potencial elétrico varia ao longo do eixo x como mostrado no gráfico da Fig.. Dos intervalos mostrados (nāo considere o comportamento das extremidades dos intervalos), determine aquele