Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.8 - Ex. 53
Um bloco de 10,0 g com uma carga de é submetido a um campo elétrico . Determine (a) o módulo e (b) a orientação (em relação ao semieixo x positivo) da força eletrostática que age sobre o bloco. Se o bloco é liberado na origem, a partir do repouso, no instante t = 0, determine (c) acoordenada x e (d) a coordenada y do bloco no instante t = 3,00 s.
Passo 1
Se a gente tem a carga e tem o campo, a gente tem a força eletrostática, certo? É só usar a equação:
Agora que a gente tem a força, calcular o módulo é moleza. O módulo nada mais é do que pegar cada componente, elevar ao quadrado, somar tudo, e depois tirar a raiz quadrada. Assim:
Passo 2
Povo bonito, entendam isso: quando a questão pede a orientação ou direção, o que ela tá te pedindo, na verdade, é o ângulo que faz com o eixo x ou o eixo y. Nessa questão, a gente tem que falar o ângulo que faz com o eixo x, na parte positiva:
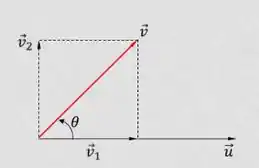
Por exemplo, o vetor faz um ângulo com o eixo horizontal. A gente começa pegando a tangente:
Agora a gente aplica a função trigonométrica inversa
E isso dá, usando uma calculadora, ou -0,197 radianos.
Passo 3
Para os itens (c) e (d), vamos precisar lembrar daquela fórmula lá da cinemática:
Vocês lembram desta? O famoso sorvetão. Vamos precisar de duas equações desta, uma para o eixo x e uma para o eixo y:
e
Só que agora a gente precisa achar e . Como fazer isso? Super simples:
Ou seja:
Daí tiramos que e . Agora é moleza, né, galera?
Resposta
Letra (a): 0,245 NLetra (b):
Letra (c): 108 mLetra (d): -21,6 m