Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Oscilações, Ondas e Termodinâmica- Ed: 5º - Capítulo 13.Problemas - Ex. 55

Um bloco de 2,00 kg está pendurado por um cabo de borracha. O bloco é suportado de forma que o cabo não esteja esticado. O comprimento não esticado do cabo é de 0,500 m, e sua massa é 5,00 g. A "constante de elasticidade" para o cabo é 100 N/m. O bloco é liberado e para momentaneamente no ponto mais baixo. (a) Determine a tensão no cabo quando o bloco está neste ponto mais baixo. (b) Qual é o comprimento do cabo nesta posição "esticada"? (c) Se o bloco é mantido nesta posição mais baixa, encontre a velocidade de uma onda transversal no cabo.

Passo 1

Alô Alô beleuzaaaaa, vamo pra mais uma resolução???

Então encoxxxtaaaa

Primeiramente, iremos analisar a situação inicial e final por meio da figura a seguir:

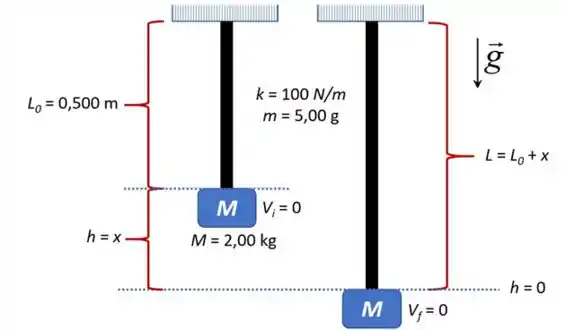
Escolheremos a altura nula (=0) no ponto mais baixo (à direita na figura).

Usando conservação da energia mecânica, iremos obter:

E M ,   i = E M ,   f → M ⋅ g ⋅ x = k ⋅ x 2 2

x = 2 ⋅ M ⋅ g k = 2 ⋅ 2,00 ⋅ 9,8 100 = 0,392   m

Passo 2

  1. Portanto, a força de tensão no cabo valerá

    2. f = F e l = k ⋅ x = 100 ⋅ 0,392 = 39,2   N .

    Passo 3

  2. Podemos calcular o comprimento do cabo por meio da seguinte equação:

    3. L = L 0 + x = 0,500 + 0,392 = 0,892   m

    Passo 4

  3. Podemos definir a velocidade de uma onda transversal da seguinte maneira:

μ = m L

μ = 5 × 10 - 3 0,892

μ = 5,61 × 10 - 3   k g / m

V = f μ

V = 39,2 5,61 × 10 - 3

V = 83,6   m / s

Resposta

  1. f   =   39,2   N .

  2. L   =   0,892   m

  3. V = 83,6   m / s
Ver Outros Exercícios desse livro