Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.1 - Ex. 7
Um bloco de cobre de cuja temperatura é é colocado em uma caixa isolada juntamente com um bloco de chumbo de cuja temperatura é . Qual é a temperatura de equilíbrio do sistema dos dois blocos? (b) Qual é a variação da energia interna do sistema do estado inicial para o estado de equilíbrio? (c) Qual é a variação da entropia do sistema? (Sugestão: consulte a tabela .)
Passo 1
(a) Faala ae, beleza?? Bora resolver esse exercício.
Para calcular a temperatura de equilíbrio do sistema, a gente precisa lembrar do seguinte: em um sistema isolado, a soma das trocas de calor é igual a zero!
Agora vamos substituir as fórmulas para o calor trocado ( vai representar o cobre e o chumbo):
Vamos isolar a temperatura , que é o que queremos encontrar:
Passo 2
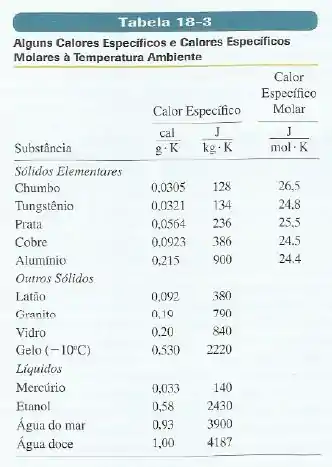
Ótimo, agora podemos substituir os valores. Já que as massas estão em gramas, vamos usar o calor específico em , pegando na tabela 18-3:
Passo 3
(b) Voltando lá no enunciado, encontramos um termo muito importante: “uma caixa isolada”.
Se o sistema é isolado, a variação da energia interna é nula!
Passo 4
(c) Ao invés de decorar mais uma fórmula, vamos pensar o seguinte: a variação de entropia de cada bloco é a seguinte:
Lá no passo , a gente já tinha encontrado a fórmula para o calor trocado:
E na forma diferencial:
Ótimo, se a gente substituir isso na fórmula da entropia:
Como é constante, podemos tirar da integral:
Passo 5
Agora, se queremos a variação de entropia do sistema inteiro, é só somar as variações para o cobre e para o chumbo!
Substituindo os valores:
Como a gente usou o calor específico em , essa resposta está em calorias por Kelvin!
Convertendo para Joules por Kelvin, que é o “padrão” para o cálculo de entropias:
Pronto, resolvido!
Resposta
(a)
(b)
(c) .