Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Exercício - Ex. 45

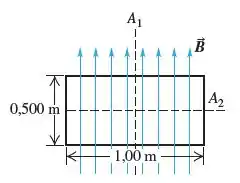
Uma bobina retangular uniforme com massa total igual a 210 g e dimensões de 0,500 m 1,00 m está orientada no sentido perpendicular a um campo magnético uniforme de 3,00 T. Uma corrente de 2,0 A é repentinamente acionada na bobina. (a) Em torno de qual eixo (A1 ou A2) a bobina começará a girar? Por quê? (b) Determine a aceleração angular inicial da bobina logo após a corrente ser acionada.

Passo 1

letra a)

O torque é dado pela expressão:

τ _ = μ _ × B _

Usando a regra da mão direita, o torque tem direção horizontal. Logo a espira irá girar em torno do eixo A2.

Passo 2

letra b)

Podemos escrever o torque em termos da aceleração angular e do momento de inércia.

τ = I α

α = τ I

Precisamos agora calcular o torque total e o momento de inércia da espira.

Passo 3

O torque será:

τ _ = μ _ × B _

τ = μ B   s e n ϕ

Como a normal do plano e o campo são perpendicular s e n ϕ = 1

τ = μ B

τ = i A B

τ = 2 ⋅ 0,5 ⋅ 1 ⋅ 3

τ = 3   N m

Passo 4

Já o momento de inércia da espira será:

I = 2 ⋅ m 1 d 1 2 + 2 ⋅ 1 12 m 0,5 d 0,5 2

m 1 é a massa do fio de 1   m , que podemos encontrar como sendo um terço da massa total.

m 1 = 0,07   K g

d 1 é a distância do fio de 1   m   até o eixo de rotação.

d 1 = 0,25   m

m 2 é a massa do fio de 0,5   m , que podemos encontrar como sendo a metade da massa de m 1 .

m 2 = 0,035   K g

d 2 é a distância do fio de 0,5   m   até o eixo de rotação.

d 2 = 0,5   m

Logo:

I = 2 ⋅ 0,07 ⋅ 0,25 2 + 2 ⋅ 1 12 ⋅ 0,035 ⋅ 0,5 2

I = 10,2 ⋅ 10 - 3   K g m 2

Passo 5

A aceleração será:

α = 3 10,2 ⋅ 10 - 3

α = 290   r a d / s 2

Resposta

letra a) A2.

letra b) α = 290   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma única espira circular possui 10,0 cm de diâmetro e conduz uma corrente de 2,00 A. (a) Qual é o campo magnético no centro dessa espira? (b) Suponha que agora conectemos 1.000 dessas espiras em séri
Uma bobina circular com 800 espiras enroladas de modo compacto possui raio de 2,40 cm. (a) Qual deve ser a corrente que passa pela bobina, supondo que o campo magnético no centro da bobina seja igual
Duas espiras de fio circulares concêntricas encontram- -se sobre uma mesa, uma dentro da outra. O fio interno possui um diâmetro de 20,0 cm e conduz uma corrente de 12,0 A em sentido horário, conforme
Para usar uma amostra maior, os experimentadores constroem um solenoide com o mesmo comprimento, tipo de fio e espaçamento de espiras, mas com o dobro do diâmetro do original. Qual é a relação entre o
Que corrente é necessária no fio para que o campo magnético experimentado pela bactéria tenha um módulo de 150μ T ?0,095 A; 0,12 A; 0,30 A; 14 A.