Uma caixa está deslizando em um plano inclinado com ângulo de 15° em relação a horizontal. O coeficiente de atrito cinético entre a caixa e a superfície inclinada é de 0,18. A velocidade inicial da caixa no início do plano inclinado é de 1,50 m/s. Quão longe a caixa irá percorrer no plano inclinado até parar?
Passo 1
E aí gente, tudo bem? Vamos fazer um desenho!!!
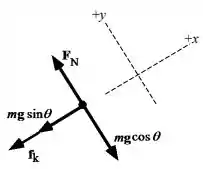
Passo 2
Resolvendo a equação 3.6ª do livro, podemos encontrar o deslocamento sendo dado por:
Sabemos que na direção x, temos que:
Para o eixo y, temos:
E sabemos quem é nossa força de atrito cinético, certo?
Passo 3
Portanto, resolvendo a equação em
Nós podemos substituir essa expressão para na equação do deslocamento do passo (1) e encontrar que: