Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 3.Exercícios e Problemas - Ex. 14
Calcule as componentes do vetor da figura 3.5 no sistema de coordenadas .
Passo 1
Salve pessoas, tudo certo? Vamos lá! Primeiro, temos que a figura 3.5 trata-se desse esquema de vetores:
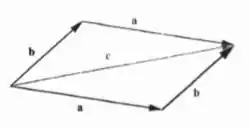
Então sem enrolar, bora calcular!
Passo 2
A definição de e trata-se das componentes auxiliares do vetor, tratados pelo módulo, menos a componente de vetor . Logo, se as componentes são (para o ) e (para o ), basta pegarmos os dados da questão anterior e subtrairmos. Logo,
Resposta
e
Resposta
Exercícios de Livros Relacionados
Faça gráficos das coordenadas x ( t ) , y ( t ) e z ( t ) do corpo cujo movimento é descrito no problema 4.3.
Um corpo move-se segundo a fórmula r = 20 m / s i ⋅ t - 4.9 m / s 2 t 2 j + 20 m s t k Trata-se de um movimento em um plano?
A posição de um corpo em movimento varia no tempo segundo a equação r = 80 + 15 t + 3 t 2 i - 5 t 2 j + 20 t k Onde as distancias são medidas em metros e o tempo é medido em segundos. Calcule (A) a ve
Um corpo está no instante inicial t = 0 , na posição r 0 = i 3 m + k 5 m e com velocidade v o = j 7 m / s . Sua aceleração evolui no tempo segundo a t = - j 10 m s 2 + k 3 t m s 3 . Calcule (A) a posi