Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 3.Exercícios e Problemas - Ex. 13
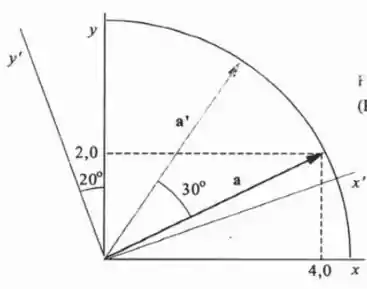
Calcule as componentes do vetor a no sistema de coordenadas .
Passo 1
Para saber as novas coordenadas do vetor a, precisaremos rotacionar o eixo!!!
Fazendo uso da eq. 3.46, sabemos que, após uma rotação do eixo em graus, as novas coordenadas de um vetor genérico u passam a ser dadas por:
Portanto:
Resposta
Exercícios de Livros Relacionados
Os vetores a → e b → da Fig. 3-28 têm o mesmo módulo, 10,0m , e os ângulos mostrados na figura são θ 1 = 30 ° e θ 2 = 105 ° . Determine as componentes (a) x e (b) y da soma vetorial r → dos dois vetor
Determine as componentes (a) x , (b) y e (c) z da soma r → dos deslocamentos c → e d → cujas componentes em metros ao longo dos três eixos são c x = 7,4 , c y = - 3,8 , c z = - 6,1 , d x = 4,4 , d y =
Três vetores, a → , b → e c → , têm o mesmo módulo, 50m , e estão em um plano x y . Os ângulos dos vetores em relação ao semieixo x positivo são 30 ° , 195 ° , e 315 ° , respectivamente. Determine (a)
Em um jogo de xadrez ao ar livre, no qual as peças ocupam o centro de quadrados com 1,00m de lado, um cavalo é movido da seguinte forma: (1) dois quadrados para a frente e um quadrado para a direita;
Se B → é somado a C → = 3 i ^ + 4 j ^ , o resultado é um vetor no sentido do semi-eixo y positivo, com um módulo igual ao de C → . Qual o módulo de B → ?