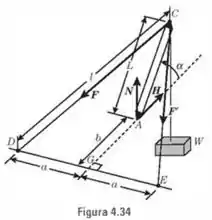
Calcule as forças , , e da Fig. 4.34. e são cabos. Despreze o peso da haste .
Passo 1
E aí, beleza?? Vamos começar definindo um sistema de eixos. A origem do sistema será o ponto , o eixo coincidirá com o segmento de reta , o eixo com o segmento de reta e o eixo será o eixo perpendicular a ambos, apontando para cima. Desse modo, vamos localizar alguns pontos relevantes:
Passo 2
Desse modo, podemos escrever as forças vetorialmente:
Passo 3
Assim, vamos calcular o torque em relação ao ponto . A distância do ponto de aplicação das três forças atuantes na barra que geram torque ao ponto é:
Assim:
Portanto:
Assim, note que, ao somar esses três vetores, devemos obter o vetor nulo como resposta. Assim, analisando apenas o eixo , ou o , podemos concluir:
Portanto, . Assim, analisando o eixo , vem:
Logo:
Passo 4
Agora, somando as forças atuantes na barra, temos:
Assim: