Enunciado
Física - Eisberg e Resnick - Física quântica- Ed: 1º - Capítulo 5.Problemas - Ex. 14
a) Calcule os valores esperados da energia cinética e da energia potencial para uma partícula no estado de menor energia de um oscilado harmônico simples, usando a função de onda do exemplo 5-7.
b) Compare com as médias no tempo das energias cinética e potencial para um oscilador harmônico simples clássico com a mesma energia total.
Passo 1
Fala galerinha, beleza?
A função de onda para o estado fundamental do oscilador harmônico foi discutida no exemplo 5-7 do livro:
O valor esperado da energia cinética é dado por
Assim,
Já o valor esperado da energia potencial é
Portanto,
Calcular essas integrais não será tarefa fácil, mas a física do problema acaba aqui, o resto é matemática!
Passo 2
Primeiro vamos derivar com relação a :
Agora usamos a regra do produto para tomar a segunda derivada:
Portanto,
Mas lembre-se que
Logo,
Assim,
Para resolver essa integral, vamos fazer a substituição
Assim,
Substituindo a expressão de :
Portanto,
Para fazer a integral, recorremos ao WOLFRAM digitando
Ele nos devolve:
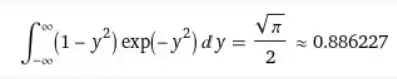
Assim,
Ou ainda,
Lembre-se que a energia do estado fundamental do oscilador harmônico obtida no exemplo 5-7 é
Passo 3
Já para o potencial, temos
Fazemos novamente a substituição
Assim,
Ou ainda,
Novamente, recorremos ao WOLFRAM:
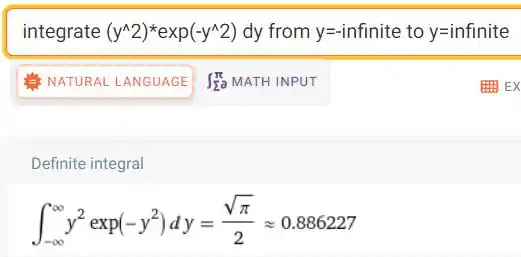
Assim,
Passo 4
Observe que
Os valores esperados da energia cinética e potencial são iguais entre si e, consequentemente, são iguais a metade da energia total pois
Para um oscilador harmônico clássico com solução e , temos
Lembre-se que . Assim, a energia total é dada por
Considerando as médias temporais e que , temos
Portanto, a relação vale tanto para o sistema clássico como para o sistema quântico.