Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Oscilações, Ondas e Termodinâmica- Ed: 5º - Capítulo 13.Problemas - Ex. 53

Caminhões que transportam lixo para o aterro sanitário da cidade formam uma procissão quase constante em uma estrada rural, todos viajando a 19,7 m/s na mesma direção. Dois caminhões chegam ao aterro a cada 3 min. Um ciclista também está viajando em direção ao aterro, a 4,47 m/s. (a) Com que frequência os caminhões passam o ciclista? (b) E se? Uma colina não diminui a velocidade dos caminhões, mas faz que a velocidade do ciclista fora de forma caia para 1,56 m/s. Qual é a frequência com que os caminhões passam o ciclista agora?

Passo 1

Alô Alô beleuzaaaaa, vamo pra mais uma resolução???

Então encoxxxtaaaa

Se consideramos que 2 caminhões chegam ao aterro a cada três minutos, então em uma hora (60 minutos) chegam 40 caminhões. A figura a seguir representa a fileira dos 40 caminhões que chegarão ao aterro na próxima hora:

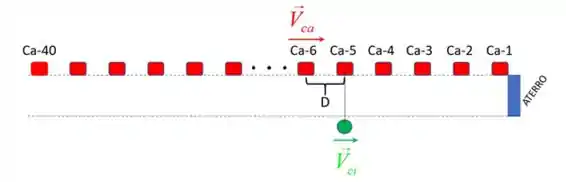
O ciclista (círculo) está sendo ultrapassado pelo caminhão 5 (Ca-5) e , em breve, será ultrapassado pelo caminhão (Ca-6). Nosso objetivo será calcular o intervalo de tempo necessário para que essa nova ultrapassagem ocorra.

Passo 2

Considerando caminhões e o ciclista como pontos materiais em movimento uniforme, as funções horárias do caminhão 6 e do ciclista serão, respectivamente:

S C a = V C a ⋅ t

S C i = D + V C i ⋅ t

No encontro, teremos:

S C a = S C i → V C a ⋅ t = D + V C i ⋅ t

Logo,

t u l t r a p a s s a g e m = D V C a - V C i

Passo 3

Pode se notar que precisamos do valor de D, ou seja, da distância entre os caminhões ou, de forma equivalente, da distância que cada caminhão percorre em 1,5 minutos:

V = D ∆ t

D = 19,7 ⋅ 90

D = 1773   m

D = 1,773   k m

Passo 4

Substituindo o valor encontrado, na expressão do tempo de ultrapassagem, iremos obter:

t u l t r a p a s s a g e m = D V C a - V C i

t u l t r a p a s s a g e m = 1,773 19,7 ⋅ 3,6 - 4,47 ⋅ 3,6

t u l t r a p a s s a g e m = 0,03233   h

O tempo resultou em horas porque usamos a velocidade em km/h, e a distância em km.

Passo 5

  1. Para podemos obter a frequência com que o ciclista é ultrapassado, basta perceber que o intervalo de tempo calculado acima corresponde ao período de ultrapassagem. Como a frequência é o inverso do período, iremos obter:

    2. f = 1 T

    f = 1 0,03233

    f = 31   c a m i n h o õ e s / h o r a

    Passo 6

  2. A única mudança se deu na velocidade do ciclista e , por isso, o novo tempo de ultrapassagem e a nova frequência seriam obtidos da seguinte maneira:

t u l t r a p a s s a g e m = D V C a - V C i

t u l t r a p a s s a g e m = 1,773 19,7 ⋅ 3,6 - 1,56 ⋅ 3,6

t u l t r a p a s s a g e m = 0,02715   h

f = 1 T

f = 1 0,02715

f = 37   c a m i n h o õ e s / h o r a

Resposta

  1. f = 31   c a m i n h o õ e s / h o r a .
  2. f = 37   c a m i n h o õ e s / h o r a .
Ver Outros Exercícios desse livro