Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 37.Exercícios e Problemas - Ex. 12
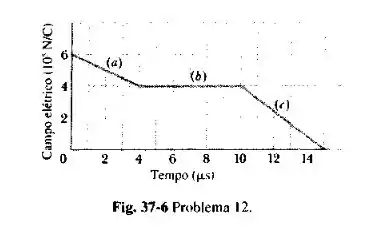
Um campo elétrico uniforme cai a zero a partir de uma intensidade inicial de num intervalo de tempo igual a , do modo indicado na Fig. 37-6. Calcular a corrente de deslocamento que atravessa uma área de ortogonal à direção do campo, durante cada um dos intervalos de tempo (a), (b) e (c), indicados no gráfico (Ignore o comportamento nas extremidades dos intervalos.)
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A - A corrente de deslocamento é dada por:
Onde é o fluxo elétrico e é igual ao campo elétrico multiplicado pela área, então:
A magnitude da corrente é, portanto
Do gráfico entre e o valor representa a inclinação do gráfico, na primeira região , temos:
A magnitude da corrente de deslocamento nesta região é:
Fazendo a substituição, nós temos que
Portanto,
Passo 2
B - A curva na região é uma linha reta, com inclinação zero, o que significa que a corrente de deslocamento é zero neste período:
C – Na região c, nós temos
Portanto, a magnitude da corrente de deslocamento nesta região é: