Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 3- Ed: 4º - Capítulo 37.Exercícios e Problemas - Ex. 13

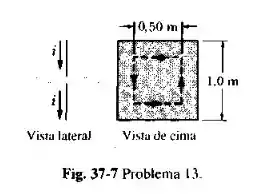
Um capacitor de placas paralelas quadradas, de 1,0   m de lado, como o da Fig. 37-7, está sendo carregado por uma corrente de 2,0   A que chega a uma das placas e sai da outra.

a. Qual é a corrente de deslocamento na região entre as placas?

b. Qual é o valor de d E / d t nesta região?

c. Qual é a corrente de deslocamento através da trajetória quadrada tracejada entre as placas?

d. Qual é o valor de ∮ B ∙ d s ao longo desta trajetória?

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

A - Suponha que temos um capacitor de placas paralelas quadradas com lado de L = 1,0   m . Em qualquer instante, a corrente de deslocamento é igual à corrente de condução, então:

I d = 2,0   A

B - O fluxo elétrico é igual ao campo elétrico multiplicado pela área do capacitor:

Φ E = E A → E = Φ E A

Pegando a derivada de tempo para ambos os lados para obter:

d E d t = 1 A d Φ E d t

Mas a corrente de deslocamento é dada por:

I d = ε 0 d Φ E d t

Com isso, nós temos que

d Φ E d t = I d ε 0

Fazendo as devidas substituições

d E d t = I d ε 0 A

Como A está definida como L 2

d E d t = I d ε 0 L 2

Fazendo a substituição dos termos

d E d t = 2,0   A 8,85 × 10 - 12 F m 1,0   m 2 = 2,3 × 10 11   V / ( m ∙ s )

Portanto,

d E d t = 2,3 × 10 11   V / ( m ∙ s )

Passo 2

C - A corrente de deslocamento através do caminho quadrado com lado de d = 0,50   m , é igual à razão das áreas multiplicadas com a corrente de deslocamento através de todo o capacitor:

I d ' = d 2 L 2 I d

Fazendo a substituição, nós temos que

I d ' = 0,50 2 1,0   m 2 2,0   A = 0,50   A

Passo 3

D- A lei de Ampere-Maxwell em termos da corrente de deslocamento é dada por:

∮ B → ∙ d s → = μ 0 I d , e n c + μ 0 I e n c

Dentro do quadrado não há corrente regular fechada, então a lei se reduz a:

∮ B → ∙ d s → = μ 0 I d , e n c

Mas como I d ,   e n c = I d ' , então podemos usar de substituição direta, para esse caso

∮ B → ∙ d s → = 4 π × 10 - 7   T ∙ m A 0,50   A = 6,3 × 10 - 7   T ∙ m

Resposta

a )   I d = 2,0   A

b )   d E d t = 2,3 × 10 11   V / ( m ∙ s )

c )   I d ' = 0,50   A

d )   ∮ B → ∙ d s → = 6,3 × 10 - 7   T ∙ m

Exercícios de Livros Relacionados

Considere a direção e o sentido do campo magnético e do campo elétrico indicados a seguir. Para cada caso, quais são a direção e o sentido da propagação da onda? (a) na direção x, na direção y; (b) na
Uma onda eletromagnética senoidal está se propagando no vácuo no sentido z. Se em um dado instante e em um dado ponto do espaço o campo elétrico estiver no sentido x e possuir módulo de 4,00 V/m, quai
Considere a direção e o sentido do campo magnético e do campo elétrico indicados a seguir. Para cada caso, quais são a direção e o sentido de propagação da onda?
Como instrutor em um laboratório de física, você realiza um experimento com ondas estacionárias de micro- -ondas, semelhante às ondas estacionárias produzidas em um forno de micro-ondas doméstico. Um
Uma corda de comprimento igual a 1,50 m é esticada entre dois suportes com uma tensão tal que a velocidade da onda transversal é igual a 62,0 m/s. Calcule o comprimento de onda e a frequência: (a) do